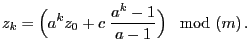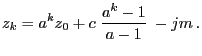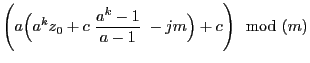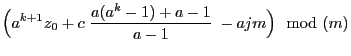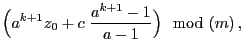Next: Statistical Tests
Up: Generation of Pseudo-Random Numbers
Previous: Simple Applications; Monte-Carlo Estimators
Contents
Linear Congruential Generators
- Most simulation algorithms are based on standard random number
generators,
- whose goal is to generate sequences
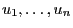 of numbers in
the unit interval
of numbers in
the unit interval ![$ (0,1]$](img165.png) . These are the so-called standard
pseudo-random numbers,
. These are the so-called standard
pseudo-random numbers,
- which can be regarded as realizations of independent and on
![$ (0,1]$](img165.png) uniformly distributed random variables
uniformly distributed random variables
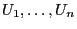 .
.
- A commonly established procedure to generate standard pseudo-random
numbers is the following linear congruential method,
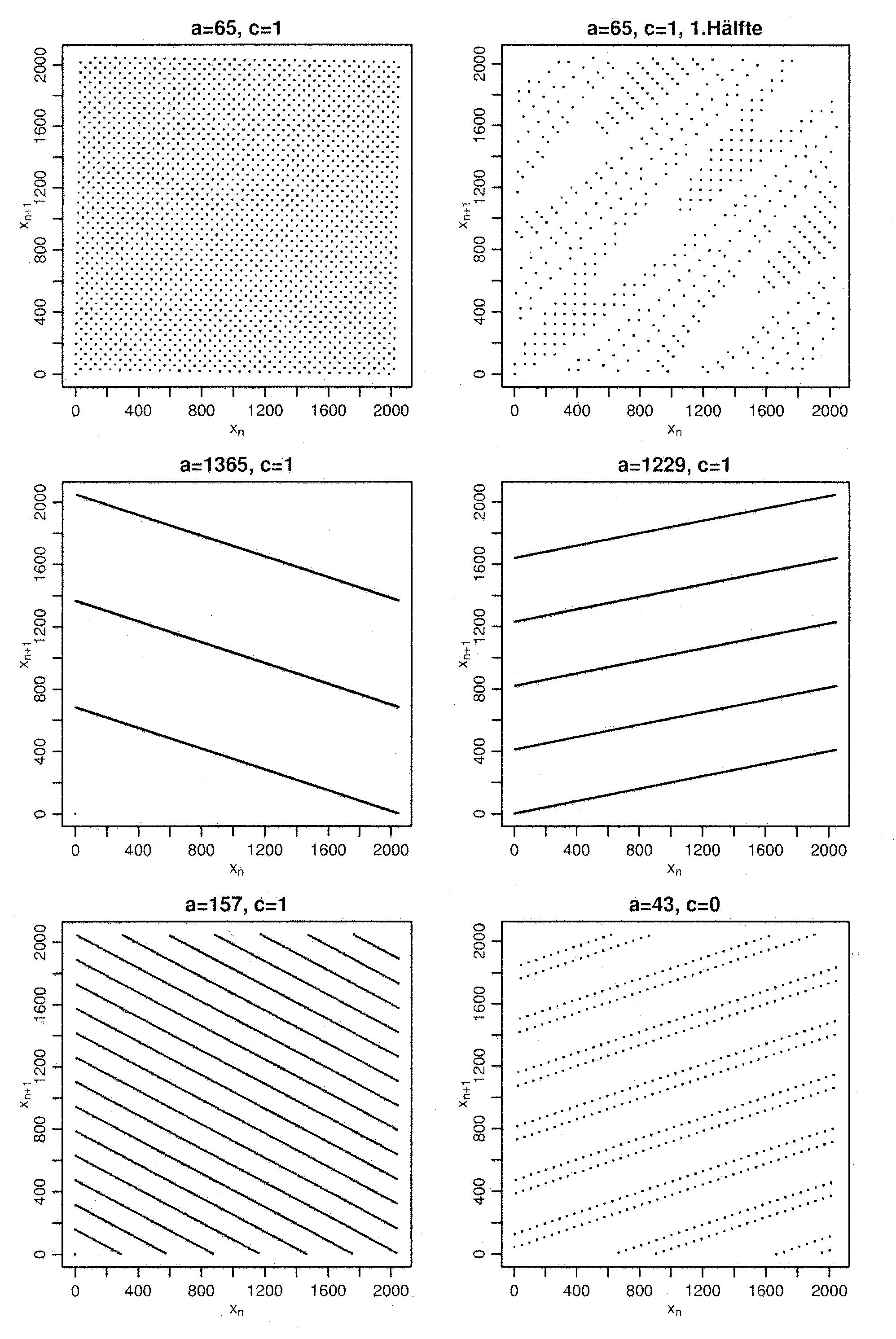
As a next step we will solve the recursion equation
(1), i.e., we will show how the number 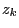 that
has been recursively defined in (1) can be
expressed directly by the initial value
that
has been recursively defined in (1) can be
expressed directly by the initial value 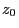 and the
parameters
and the
parameters 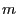 ,
, 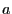 and
and 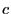 .
.
- Proof
-
- Remarks
-
We will now mention some (sufficient and necessary) conditions for
the parameters 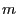 ,
, 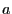 ,
, 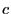 and
and 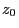 , respectively, ensuring
that the maximal possible period
, respectively, ensuring
that the maximal possible period 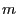 is obtained.
is obtained.
A proof of Theorem 3.2 using results from
number theory (one of them being Fermat's little theorem) can be
found e.g.
- in Section 2.7 of B.D. Ripley Stochastic Simulation, J.
Wiley & Sons, New York (1987) or
- in Section 3.2 of D.E. Knuth (1997) The Art of Computer
Programming, Vol. II, Addison-Wesley, Reading MA.
- We also refer to these two texts for the discussion
- of other generators for standard pseudo-random numbers like
nonlinear congruential generators, shift-register generators and
lagged Fibonacci generators as well as their combinations,
- alternative conditions for the parameters
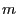 ,
, 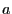 ,
, 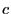 and
and 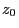 of
the linear congruential generator defined in (1),
of
the linear congruential generator defined in (1),
- ensuring the generation of sequences
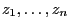 whose period
whose period
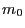 is as large as possible and also exhibiting other desirable
properties.
is as large as possible and also exhibiting other desirable
properties.
- One of those properties is
- that the points
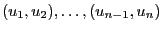 formed by pairs
of consecutive pseudo-random numbers
formed by pairs
of consecutive pseudo-random numbers 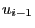 ,
, 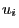 are
uniformly spread over the unit square
are
uniformly spread over the unit square ![$ [0,1]^2$](img1122.png) .
.
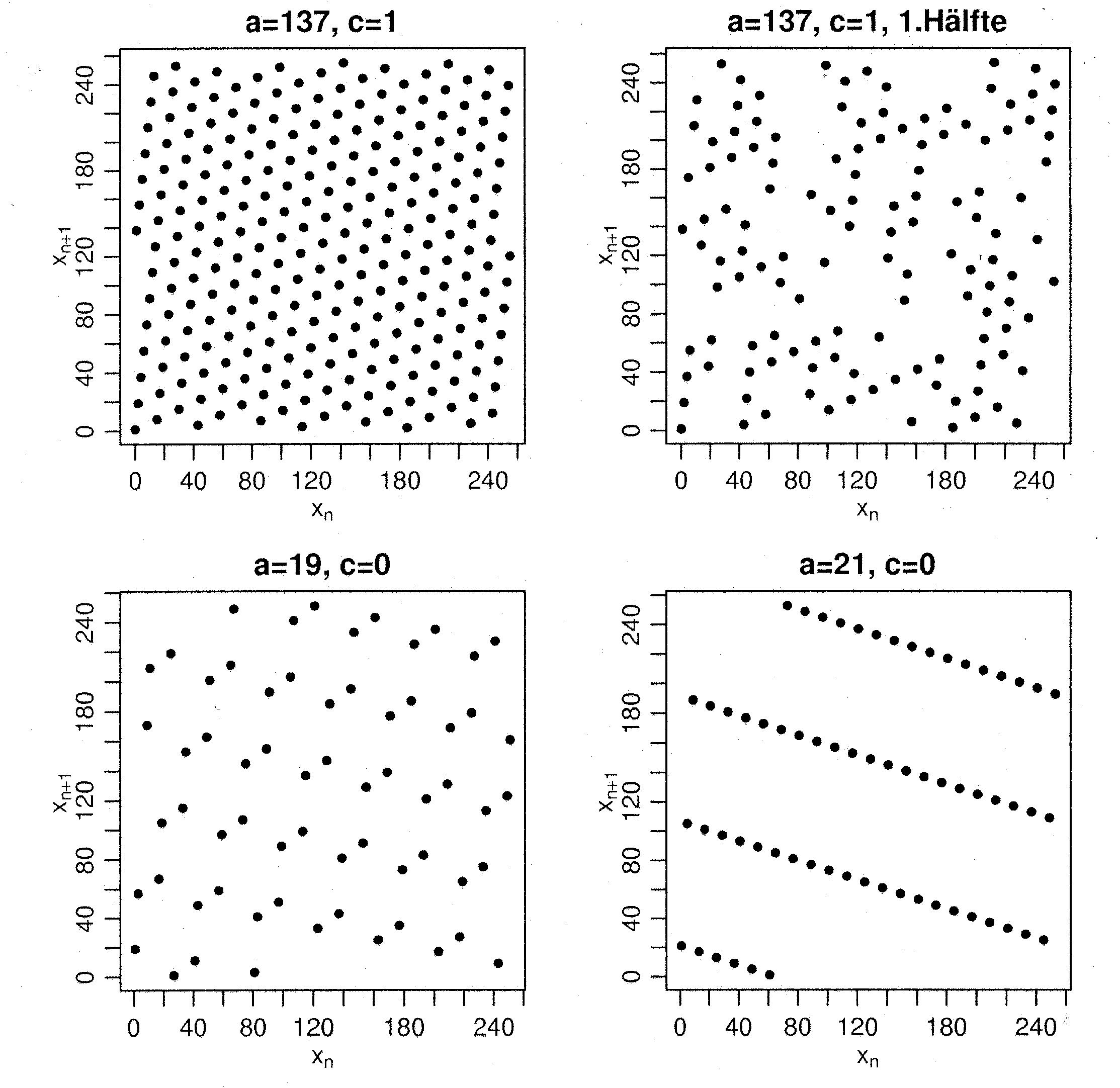
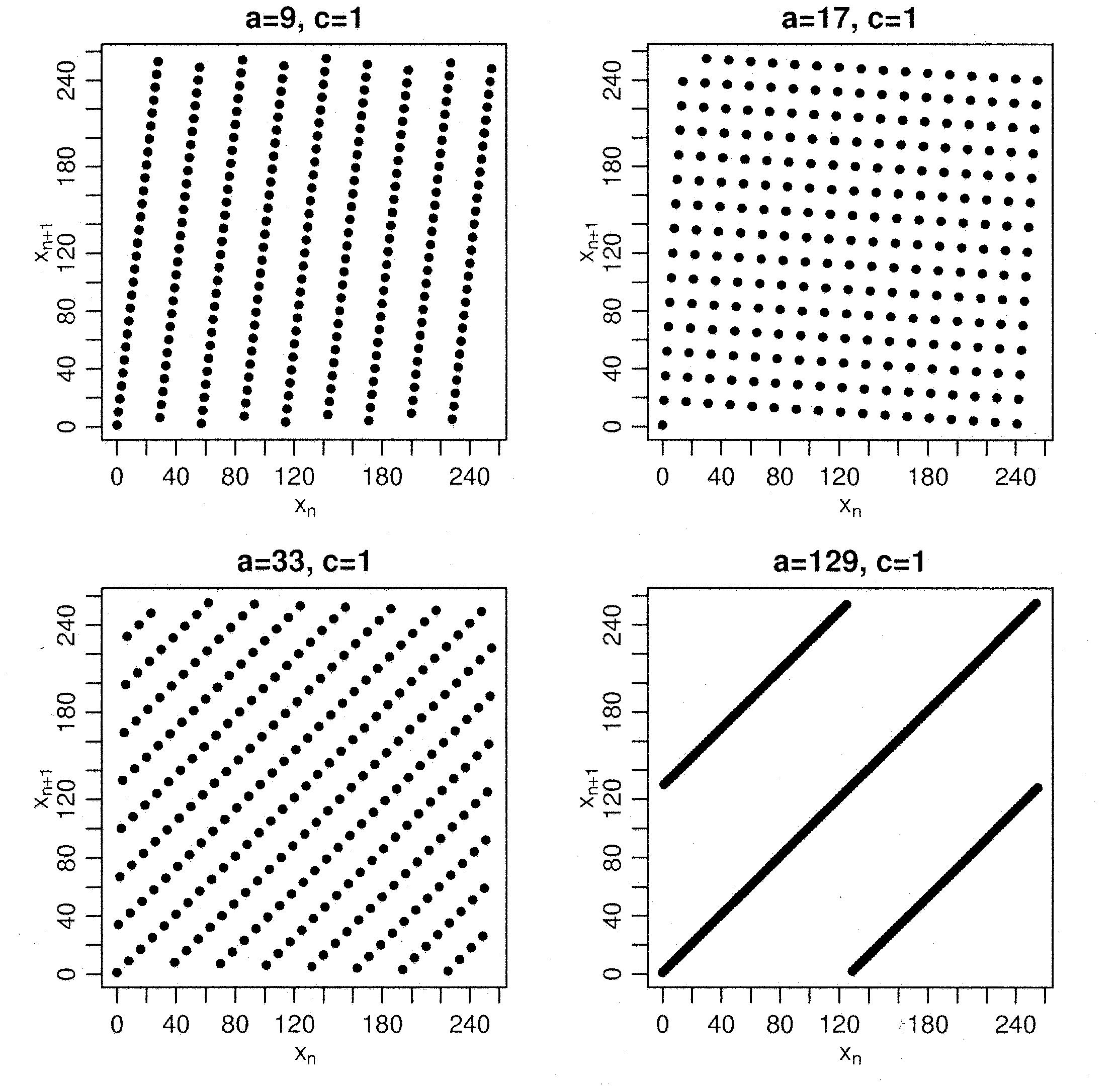
- The following numerical examples illustrate that relatively small
changes of the parameters
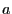 and
and 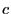 can result in completely
different point patterns
can result in completely
different point patterns
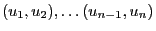 .
.
- Further details can be found in the text by Ripley (1987) that has
been already mentioned and in the lecture notes by H. Künsch
(ftp://stat.ethz.ch/U/Kuensch/skript-sim.ps) that also contains the
following figures.
Figure 3:
Point patterns for pairs
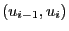 of consecutive
pseudo-random numbers for
of consecutive
pseudo-random numbers for 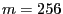
|
|
Figure 4:
Point patterns for pairs
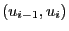 of consecutive
pseudo-random numbers for
of consecutive
pseudo-random numbers for 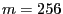
|
|
Figure 5:
Point patterns for pairs
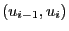 of consecutive
pseudo-random numbers for
of consecutive
pseudo-random numbers for 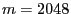
|
|




Next: Statistical Tests
Up: Generation of Pseudo-Random Numbers
Previous: Simple Applications; Monte-Carlo Estimators
Contents
Ursa Pantle
2006-07-20
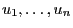 of numbers in
the unit interval
of numbers in
the unit interval ![$ (0,1]$](img165.png) . These are the so-called standard
pseudo-random numbers,
. These are the so-called standard
pseudo-random numbers,
![$ (0,1]$](img165.png) uniformly distributed random variables
uniformly distributed random variables
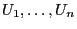 .
.
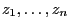 are generated
according to a recursion formula
are generated
according to a recursion formula
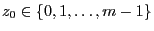 the algorithm is
starting from is called germ of the linear congruential
generator.
the algorithm is
starting from is called germ of the linear congruential
generator.
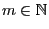 ,
,
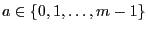 and
and
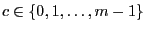 are
further parameters called modulus, factor and increment of the congruential generator.
are
further parameters called modulus, factor and increment of the congruential generator.
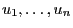 .
.