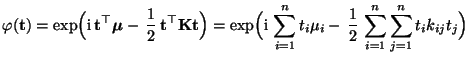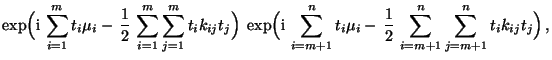Next: Lineare Transformation von normalverteilten
Up: Multivariate Normalverteilung
Previous: Charakteristiken der multivariaten Normalverteilung
Contents
Randverteilungen und Unabhängigkeit von Teilvektoren;
Faltungsstabilität
- Ein weitere interessante Eigenschaft, die ebenfalls mit Hilfe von
Theorem 3.8 hergeleitet werden kann, besteht darin,
daß beliebige Teilvektoren von normalverteilten Zufallsvektoren
erneut normalverteilt sind.
- Dabei setzen wir so wie bisher voraus, daß
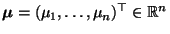 ein beliebiger Vektor
und
ein beliebiger Vektor
und
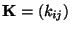 eine symmetrische und positiv definite
eine symmetrische und positiv definite
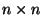 -Matrix ist.
-Matrix ist.
- Es ist klar, daß der Zufallsvektor
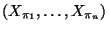 für jede Permutation
für jede Permutation
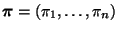 der natürlichen
Zahlen
der natürlichen
Zahlen
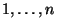 normalverteilt ist, falls
normalverteilt ist, falls
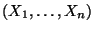 normalverteilt ist.
normalverteilt ist.
- Bei der Untersuchung der Verteilung von Teilvektoren
normalverteilter Zufallsvektoren können wir uns somit o.B.d.A. auf
die Betrachtung der ersten Komponenten beschränken.
Korollar 3.2

Falls
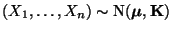
, dann gilt
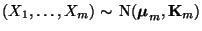
für jedes
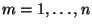
, wobei
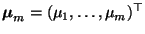
und
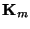
diejenige
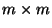
Matrix bezeichnet, die aus den
ersten
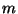
Zeilen bzw. Spalten von
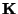
gebildet wird.
- Beweis
-
Bei der Zerlegung des normalverteilten Zufallsvektors
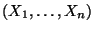 in die zwei Teilvektoren
in die zwei Teilvektoren
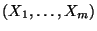 und
und
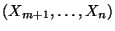 , wobei
, wobei 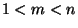 , läßt sich ein einfaches
Kriterium dafür angeben, daß
, läßt sich ein einfaches
Kriterium dafür angeben, daß
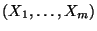 und
und
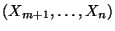 unabhängig sind.
unabhängig sind.
Korollar 3.3
- Sei
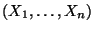 ein normalverteilter Zufallsvektor mit
ein normalverteilter Zufallsvektor mit
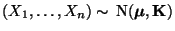 ;
;
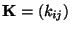 .
.
- Die Teilvektoren
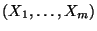 und
und
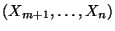 sind genau dann unabhängig, wenn
sind genau dann unabhängig, wenn 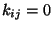 für beliebige
für beliebige
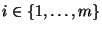 und
und
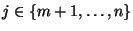 .
.
- Beweis
-
- Beachte
-
- Wir diskutieren nun noch die Faltungsstabilität der multivariaten
Normalverteilung und verallgemeinern dabei Korollar WR-3.2, wo
wir diese Eigenschaft für die eindimensionale Normalverteilung
bewiesen hatten.
- In diesem Zusammenhang ist die folgende Formel für die
charakteristische Funktion von Summen unabhängiger Zufallsvektoren
nützlich, die sich genauso wie die in Theorem WR-5.18 für den
eindimensionalen Fall hergeleitete Formel beweisen läßt.
Lemma 3.10
Seien
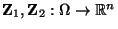
unabhängige
Zufallsvektoren. Für die charakteristische Funktion
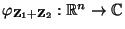
der Summe
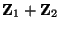
gilt dann
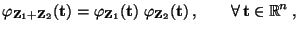 |
(46) |
wobei
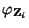
die charakteristische Funktion von
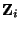
bezeichnet;
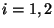
.
Die folgende Aussage wird Faltungsstabilität der
multivariaten Normalverteilung genannt.
Korollar 3.4
- Seien
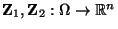 unabhängige Zufallsvektoren
mit
unabhängige Zufallsvektoren
mit
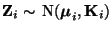 für
für 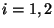 .
.
- Dann gilt
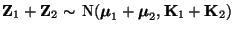 .
.
- Beweis
-
- Aus (42) und (46) ergibt sich, daß
- Hieraus und aus dem Eindeutigkeitssatz für charakteristische
Funktionen von Zufallsvektoren ergibt sich die Behauptung.





Next: Lineare Transformation von normalverteilten
Up: Multivariate Normalverteilung
Previous: Charakteristiken der multivariaten Normalverteilung
Contents
Ursa Pantle
2003-03-10
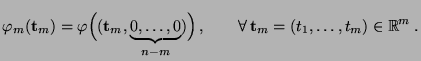
![]() in die zwei Teilvektoren
in die zwei Teilvektoren
![]() und
und
![]() , wobei
, wobei ![]() , läßt sich ein einfaches
Kriterium dafür angeben, daß
, läßt sich ein einfaches
Kriterium dafür angeben, daß
![]() und
und
![]() unabhängig sind.
unabhängig sind.