



Next: Ereignissysteme
Up: Ereignisse und Wahrscheinlichkeiten
Previous: Ereignisse und Wahrscheinlichkeiten
Contents
Ereignisse als Mengen
Wir modellieren Ereignisse als Mengen. Dabei ist eine Menge
eine Zusammenfassung von wohldefinierten und unterscheidbaren
Dingen (Elemente) zu einem Ganzen.
- Schreibweise

 Grundmenge,
Grundmenge, 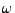 Element
Element
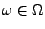 :
: 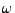 ist Element von
ist Element von 
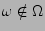 :
: 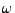 ist nicht Element von
ist nicht Element von 
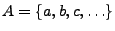 : Die Menge A besteht aus den Elementen
: Die Menge A besteht aus den Elementen
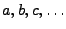
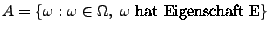 :
: 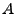 besteht aus denjenigen Elementen
besteht aus denjenigen Elementen 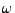 von
von  ,
die die Eigenschaft E haben.
,
die die Eigenschaft E haben.
- Beispiel

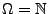 ,
,
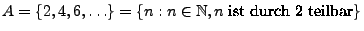
Der Vergleich von Ereignissen erfolgt durch den Vergleich
der Mengen, durch die die Ereignisse modelliert werden.
- Definition
-
-
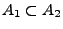 bedeutet,
bedeutet, 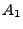 ist Teilmenge von
ist Teilmenge von 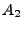 ,
d.h., aus
,
d.h., aus
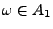 folgt
folgt
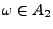
-
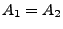 , falls
, falls
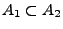 und
und
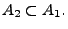
Betrachten Ereignisse, die bei einem Zufallsexperiment
(z.B. Münzwurf, Werfen eines Würfels, Roulette-Spiel, Erzeugen
einer Pseudozufallszahl mit einem Zufallszahlengenerator)
eintreten können. Dann ist
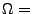 Menge aller möglichen Versuchsergebnisse (Grundmenge,
Grundgesamtheit, Merkmalraum, Stichprobenraum);
Menge aller möglichen Versuchsergebnisse (Grundmenge,
Grundgesamtheit, Merkmalraum, Stichprobenraum);
-
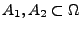 : Ereignisse = Teilmengen von
Versuchsergebnissen mit bestimmten Eigenschaften;
: Ereignisse = Teilmengen von
Versuchsergebnissen mit bestimmten Eigenschaften;
-
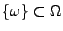 : Elementarereignis = ein (einzelnes)
Versuchsergebnis;
: Elementarereignis = ein (einzelnes)
Versuchsergebnis;
- Angenommen: bei einem Versuch wird das Ergebnis
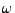 erzielt.
Dann sagen wir: Das Ereignis
erzielt.
Dann sagen wir: Das Ereignis 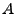 tritt ein, falls
tritt ein, falls
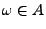 .
.
- Für
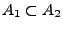 gilt: Wenn
gilt: Wenn 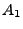 eintritt, dann tritt auch
eintritt, dann tritt auch
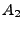 ein.
ein.
- Beispiel
- (einmaliges Würfeln):

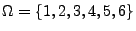 ;
Elementarereignisse
;
Elementarereignisse
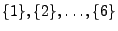 .
.
Das Ereignis 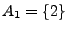 tritt genau dann ein, wenn die
Zahl 2 gewürfelt wird.
tritt genau dann ein, wenn die
Zahl 2 gewürfelt wird.
Das Ereignis
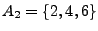 tritt genau dann ein, wenn eine gerade
Zahl gewürfelt wird.
tritt genau dann ein, wenn eine gerade
Zahl gewürfelt wird.
Also gilt:
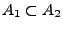 , d.h., wenn
, d.h., wenn 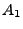 eintritt, dann tritt
auch
eintritt, dann tritt
auch 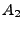 ein.
ein.
- Definition
 Diejenige Teilmenge von
Diejenige Teilmenge von  , die
kein Element enthält, heißt leere Menge und wird mit
, die
kein Element enthält, heißt leere Menge und wird mit
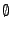 bezeichnet.
bezeichnet.
- Beachte
 Das Ereignis
Das Ereignis 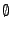 tritt niemals ein und wird
deshalb unmögliches Ereignis genannt.
tritt niemals ein und wird
deshalb unmögliches Ereignis genannt.




Next: Ereignissysteme
Up: Ereignisse und Wahrscheinlichkeiten
Previous: Ereignisse und Wahrscheinlichkeiten
Contents
Ursa Pantle
2004-05-10