



Next: Wahrscheinlichkeitsmaße
Up: Ereignisse und Wahrscheinlichkeiten
Previous: Ereignisse als Mengen
Contents
Ereignissysteme
Aus gegebenen Ereignissen
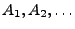 kann man durch deren
,,Verknüpfung'' weitere Ereignisse bilden. Dies wird durch die
folgenden Mengenoperationen modelliert.
kann man durch deren
,,Verknüpfung'' weitere Ereignisse bilden. Dies wird durch die
folgenden Mengenoperationen modelliert.
- Definition
-
- Vereinigungsmenge

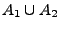 : Menge aller Elemente, die zu
: Menge aller Elemente, die zu
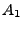 oder
oder 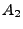 gehören.
gehören.
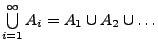 : Menge
aller Elemente, die zu mindestens einer der Mengen
: Menge
aller Elemente, die zu mindestens einer der Mengen 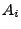 gehören.
gehören.
- Schnittmenge
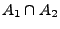 : Menge aller Elemente, die zu
: Menge aller Elemente, die zu 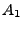 und
und 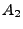 gehören.
gehören.
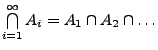 : Menge
aller Elemente, die zu jeder der Mengen
: Menge
aller Elemente, die zu jeder der Mengen 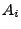 gehören.
gehören.
- Differenzmenge
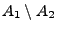 : Menge aller Elemente
von
: Menge aller Elemente
von 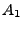 , die nicht zu
, die nicht zu 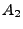 gehören.
gehören.
Spezialfall:
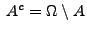 ( Komplement)
( Komplement)
- Symmetrische Mengendifferenz
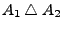 : Menge aller Elemente, die zu
: Menge aller Elemente, die zu 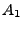 oder
oder 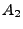 , jedoch
nicht zu beiden gehören.
, jedoch
nicht zu beiden gehören.
- Beispiel
 Sei
Sei
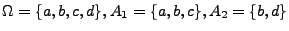 .
.
Dann gilt
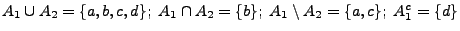 ;
;
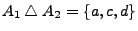 .
.
- Beachte
-
Lemma 2.1
Für beliebige Mengen
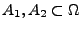
gilt:
- Beweis
 klar
klar
- Definition
 Die Mengen
Die Mengen
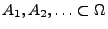 heißen
paarweise disjunkt, falls
heißen
paarweise disjunkt, falls
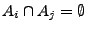 für beliebige
für beliebige
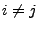 .
.
- Beachte
 Jede beliebige Folge von Mengen
Jede beliebige Folge von Mengen
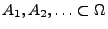 kann man in eine Folge
von paarweise disjunkten Mengen
kann man in eine Folge
von paarweise disjunkten Mengen
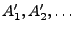 überführen:
Sei
überführen:
Sei
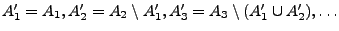
Dann gilt:
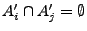 für
für 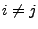 , und
, und
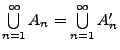
- Weitere Eigenschaften
 Sei
Sei
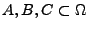 . Dann gelten
. Dann gelten
- Eindeutigkeitsgesetze:

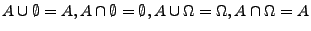
(allgemein: falls
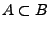 , dann gilt
, dann gilt
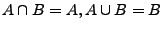 )
)
- de Morgansche Gesetze:

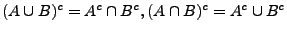
- Assoziativ-Gesetze:

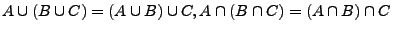
- Distributiv-Gesetze:

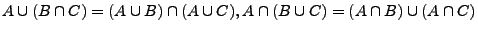
Es ist oft nicht zweckmäßig, alle möglichen Teilmengen von
 in die Modellierung einzubeziehen, sondern man betrachtet
nur die Familie derjenigen Teilmengen von
in die Modellierung einzubeziehen, sondern man betrachtet
nur die Familie derjenigen Teilmengen von  , deren
Wahrscheinlichkeiten tatsächlich von Interesse sind. Diese
Mengenfamilie soll jedoch abgeschlossen sein bezüglich der
Operationen
, deren
Wahrscheinlichkeiten tatsächlich von Interesse sind. Diese
Mengenfamilie soll jedoch abgeschlossen sein bezüglich der
Operationen
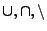 , was durch die folgende
Begriffsbildung erreicht wird.
, was durch die folgende
Begriffsbildung erreicht wird.
- Definition
 Eine nichtleere Familie
Eine nichtleere Familie
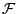 von Teilmengen
von
von Teilmengen
von 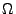 heißt Algebra, falls
heißt Algebra, falls
- (A1)
-
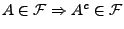
- (A2)
-
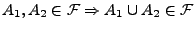
- Beispiel

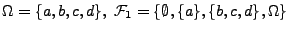 ist eine Algebra,
ist eine Algebra,
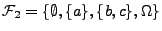 ist dagegen keine Algebra.
ist dagegen keine Algebra.
- Beweis
-
- Weil
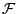 nicht leer ist, gibt es ein
nicht leer ist, gibt es ein
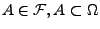 .
Also gilt
.
Also gilt
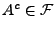 wegen (A1) bzw.
wegen (A1) bzw.
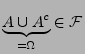 wegen (A2) bzw.
wegen (A2) bzw.
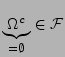 wegen (A1)
wegen (A1)
-
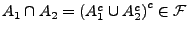
-
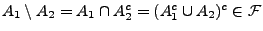
- Induktion
Um Grenzwerte bilden zu können, ist es erforderlich, dass das
Mengensystem
 nicht nur abgeschlossen ist bezüglich
Vereinigung bzw. Durchschnitt von endlich vielen Mengen,
sondern auch bezüglich Vereinigung bzw. Durchschnitt von abzählbar unendlich vielen Mengen. Dies wird durch die Hinzunahme
der folgenden Bedingung erreicht.
nicht nur abgeschlossen ist bezüglich
Vereinigung bzw. Durchschnitt von endlich vielen Mengen,
sondern auch bezüglich Vereinigung bzw. Durchschnitt von abzählbar unendlich vielen Mengen. Dies wird durch die Hinzunahme
der folgenden Bedingung erreicht.
- Definition
 Eine Algebra
Eine Algebra
 heißt
heißt 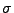 -Algebra,
falls zusätzlich
-Algebra,
falls zusätzlich
- (A3)

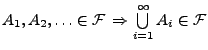 gilt.
gilt.
- Beachte
-
- Das Paar
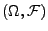 heißt Messraum, falls
heißt Messraum, falls
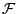 eine
eine 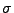 -Algebra ist.
-Algebra ist.
- Sei
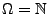 , und sei
, und sei
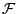 die Familie
derjenigen Teilmengen
die Familie
derjenigen Teilmengen 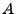 von
von
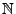 , so dass entweder
, so dass entweder 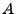 oder
oder 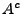 nur endlich viele Elemente hat. Das
Mengensystem
nur endlich viele Elemente hat. Das
Mengensystem
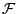 ist eine Algebra, jedoch keine
ist eine Algebra, jedoch keine
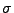 -Algebra.
-Algebra.
- Für jedes
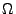 ist die Potenzmenge
ist die Potenzmenge
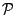 , d.h.
die Familie
aller Teilmengen von
, d.h.
die Familie
aller Teilmengen von 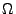 , stets eine
, stets eine 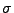 -Algebra.
-Algebra.
- Falls
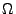 endlich oder abzählbar unendlich ist, kann
endlich oder abzählbar unendlich ist, kann
 gewählt werden. Falls
gewählt werden. Falls  nicht abzählbar ist
(z.B.
nicht abzählbar ist
(z.B.
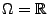 oder
oder
![$ \Omega =[0,1]),$](img108.png) dann muss eine kleinere
dann muss eine kleinere 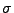 -Algebra
betrachtet werden (nicht
-Algebra
betrachtet werden (nicht
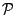 ).
).
- Definition
 Seien
Seien
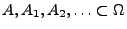 beliebige Teilmengen von
beliebige Teilmengen von
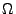 . Dann heißt die Menge
. Dann heißt die Menge
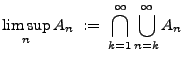 |
(1) |
der Limes Superior der Folge  , und
, und
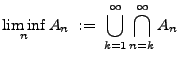 |
(2) |
heißt der Limes Inferior der Folge 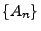 . Außerdem sagt man, dass
die Folge
. Außerdem sagt man, dass
die Folge 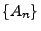 gegen die Menge
gegen die Menge 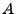 konvergiert,
falls
konvergiert,
falls
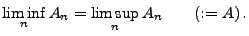 |
(3) |
- Schreibweise
 Falls die Folge
Falls die Folge 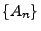 gegen die Menge
gegen die Menge 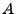 konvergiert,
d.h., falls (3) gilt, dann schreiben wir
konvergiert,
d.h., falls (3) gilt, dann schreiben wir
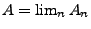 bzw. einfach
bzw. einfach 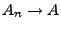 .
.
Beweis Wir zeigen nur die erste Teilaussage. Der Beweis der
zweiten Teilaussage ist analog. Sei
Wir zeigen nur die erste Teilaussage. Der Beweis der
zweiten Teilaussage ist analog. Sei
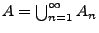 . Für jedes
. Für jedes 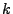 gilt dann
gilt dann
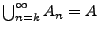 .
Also ist
.
Also ist
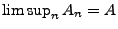 . Andererseits gilt
. Andererseits gilt
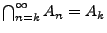 , d.h.,
, d.h.,
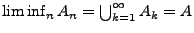 .
.





Next: Wahrscheinlichkeitsmaße
Up: Ereignisse und Wahrscheinlichkeiten
Previous: Ereignisse als Mengen
Contents
Ursa Pantle
2004-05-10
![]() kann man durch deren
,,Verknüpfung'' weitere Ereignisse bilden. Dies wird durch die
folgenden Mengenoperationen modelliert.
kann man durch deren
,,Verknüpfung'' weitere Ereignisse bilden. Dies wird durch die
folgenden Mengenoperationen modelliert.
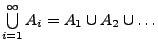 : Menge
aller Elemente, die zu mindestens einer der Mengen
: Menge
aller Elemente, die zu mindestens einer der Mengen 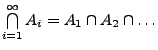 : Menge
aller Elemente, die zu jeder der Mengen
: Menge
aller Elemente, die zu jeder der Mengen 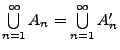
![]() in die Modellierung einzubeziehen, sondern man betrachtet
nur die Familie derjenigen Teilmengen von
in die Modellierung einzubeziehen, sondern man betrachtet
nur die Familie derjenigen Teilmengen von ![]() , deren
Wahrscheinlichkeiten tatsächlich von Interesse sind. Diese
Mengenfamilie soll jedoch abgeschlossen sein bezüglich der
Operationen
, deren
Wahrscheinlichkeiten tatsächlich von Interesse sind. Diese
Mengenfamilie soll jedoch abgeschlossen sein bezüglich der
Operationen
![]() , was durch die folgende
Begriffsbildung erreicht wird.
, was durch die folgende
Begriffsbildung erreicht wird.
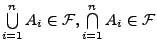
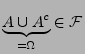 wegen (A2) bzw.
wegen (A2) bzw.
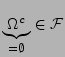 wegen (A1)
wegen (A1)
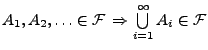 gilt.
gilt.