



Next: Unabhängige Zufallsvariable
Up: Stochastische Unabhängigkeit
Previous: Stochastische Unabhängigkeit
Contents
Unabhängige Ereignisse
Der Begriff der stochastischen Unabhängigkeit zweier Ereignisse
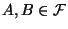 ist mit der intuitiven Vorstellung verbunden, daß die
bedingte Wahrscheinlichkeit
ist mit der intuitiven Vorstellung verbunden, daß die
bedingte Wahrscheinlichkeit
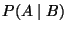 des Ereignisses
des Ereignisses 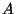 unter
der Bedingung
unter
der Bedingung 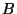 mit der ,,unbedingten'' Wahrscheinlichkeit
mit der ,,unbedingten'' Wahrscheinlichkeit
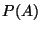 von
von 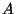 übereinstimmt, d.h.
übereinstimmt, d.h.
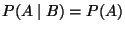 , wobei
, wobei
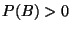 vorausgesetzt wird.
vorausgesetzt wird.
Es ist jedoch zweckmäßiger, die folgende (äquivalente) Gleichung
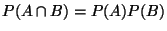 zu betrachten, weil durch sie auch der Fall
zu betrachten, weil durch sie auch der Fall
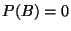 erfaßt wird.
erfaßt wird.
- Definition 3.16
-
- Die Ereignisse
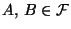 heißen unabhängig,
falls
heißen unabhängig,
falls
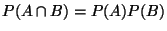 .
.
- Sei
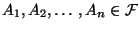 eine beliebige Folge von Ereignissen.
Dann sagt man, daß
eine beliebige Folge von Ereignissen.
Dann sagt man, daß
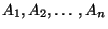 unabhängige Ereignisse sind,
falls für jede Teilfolge
unabhängige Ereignisse sind,
falls für jede Teilfolge
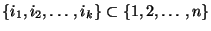 gilt:
gilt:
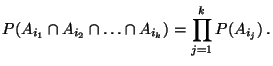 |
(18) |
- Beachte
-
- Der Begriff der Unabhängigkeit wird auch für unendliche Folgen von Ereignissen benötigt.
Man sagt, daß
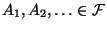 unabhängige Ereignisse sind,
falls für jede endliche Teilfolge
unabhängige Ereignisse sind,
falls für jede endliche Teilfolge
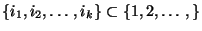 die Bedingung (18) erfüllt ist.
die Bedingung (18) erfüllt ist.
- Das folgende Beispiel zeigt, daß aus der
Unabhängigkeit von Ereignis-Paaren
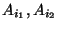 im
allgemeinen nicht die (vollständige) Unabhängigkeit der
gesamten Folge
im
allgemeinen nicht die (vollständige) Unabhängigkeit der
gesamten Folge
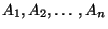 impliziert wird.
impliziert wird.
- Beispiel
-




Next: Unabhängige Zufallsvariable
Up: Stochastische Unabhängigkeit
Previous: Stochastische Unabhängigkeit
Contents
Roland Maier
2001-08-20
![]() ist mit der intuitiven Vorstellung verbunden, daß die
bedingte Wahrscheinlichkeit
ist mit der intuitiven Vorstellung verbunden, daß die
bedingte Wahrscheinlichkeit
![]() des Ereignisses
des Ereignisses ![]() unter
der Bedingung
unter
der Bedingung ![]() mit der ,,unbedingten'' Wahrscheinlichkeit
mit der ,,unbedingten'' Wahrscheinlichkeit
![]() von
von ![]() übereinstimmt, d.h.
übereinstimmt, d.h.
![]() , wobei
, wobei
![]() vorausgesetzt wird.
vorausgesetzt wird.
![]() zu betrachten, weil durch sie auch der Fall
zu betrachten, weil durch sie auch der Fall
![]() erfaßt wird.
erfaßt wird.