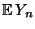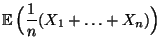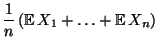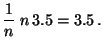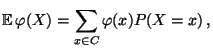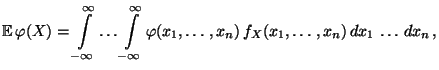- Falls
 diskret ist mit
diskret ist mit
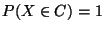 für eine
abzählbare Menge
für eine
abzählbare Menge
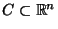 , dann gilt
, dann gilt
wobei vorausgesetzt wird, daß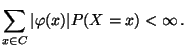
- Falls
 absolutstetig ist mit der (gemeinsamen) Dichte
absolutstetig ist mit der (gemeinsamen) Dichte 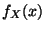 ,
dann gilt
,
dann gilt
wobei vorausgesetzt wird, daß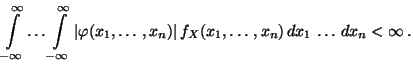
Außerdem gilt für jede Zufallsvariable
und für beliebige
- Falls
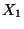 und
und 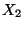 diskrete Zufallsvariablen sind, dann ergibt
sich (15) aus (13), wobei ähnlich wie
im Beweis von Lemma 4.2 vorgegangen werden kann.
diskrete Zufallsvariablen sind, dann ergibt
sich (15) aus (13), wobei ähnlich wie
im Beweis von Lemma 4.2 vorgegangen werden kann.
- Wir führen den Beweis von (15) nur für den Fall,
daß der Zufallsvektor
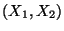 absolutstetig ist. Für
absolutstetig ist. Für
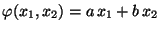 ergibt sich dann aus
(14), daß
ergibt sich dann aus
(14), daß
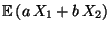

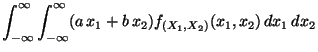

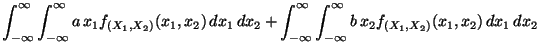

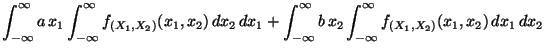

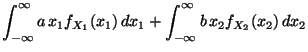

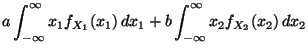

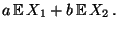
- Durch Ausmultiplizieren der quadratischen Form in
(11) ergibt sich
Var 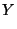

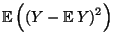

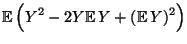

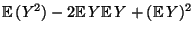

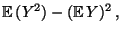
wobei sich die vorletzte Gleichung aus (15) ergibt. Damit ist (16) bewiesen. - Für
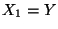 und
und 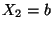 ergibt sich aus (15), daß
ergibt sich aus (15), daß
Var 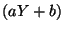

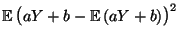

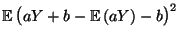

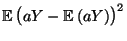

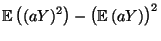

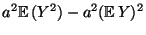

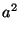 Var
Var 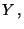
wobei sich die letzten drei Gleichungen aus (16) bzw. erneut aus (15) ergeben. Damit ist auch (17) bewiesen.
- Betrachten den Wahrscheinlichkeitsraum
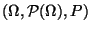 , der in
Abschnitt 4.1.1
eingeführt worden ist.
, der in
Abschnitt 4.1.1
eingeführt worden ist.
- Betrachten die Zufallsvariablen
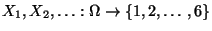 , wobei
, wobei  die
zufällige Augenzahl ist, die beim
die
zufällige Augenzahl ist, die beim 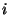 -ten Würfeln erzielt
wird.
-ten Würfeln erzielt
wird.
- Dann gilt
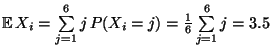 .
.
- Aus Korollar 4.6 ergibt sich dann für den Erwartungswert
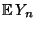 der mittleren Augenzahl
der mittleren Augenzahl
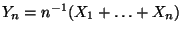 bei
bei  -maligem Würfeln
-maligem Würfeln