



Next: Parametertests bei Normalverteilung
Up: Tests statistischer Hypothesen
Previous: Tests statistischer Hypothesen
Contents
Kritischer Bereich;
Fehlerwahrscheinlichkeiten
Sei 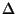 die Familie der insgesamt in Betracht gezogenen (d.h.
potentiell möglichen) Verteilungsfunktionen
die Familie der insgesamt in Betracht gezogenen (d.h.
potentiell möglichen) Verteilungsfunktionen 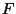 der
Stichprobenvariablen
der
Stichprobenvariablen  ;
;
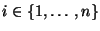 .
.
Dabei ist die folgende Sprechweise üblich:
- Die Hypothese
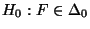 heißt Nullhypothese,
während
heißt Nullhypothese,
während
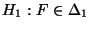 Alternativhypothese genannt
wird.
Alternativhypothese genannt
wird.
- Die Nullhypothese
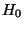 bzw. die Alternativhypothese
bzw. die Alternativhypothese 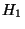 heißen
einfach, falls die Teilmenge
heißen
einfach, falls die Teilmenge 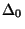 bzw.
bzw. 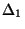 nur
aus einem Element besteht. Ansonsten sagt man, daß
nur
aus einem Element besteht. Ansonsten sagt man, daß 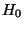 bzw.
bzw.
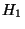 zusammengesetzte Hypothesen sind.
zusammengesetzte Hypothesen sind.
Um zwischen der Nullhypothese 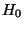 und der Alternativhypothese
und der Alternativhypothese
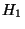 abwägen zu können, wird ein Test, d.h. eine Entscheidungsregel nach dem folgenden Prinzip konstruiert:
abwägen zu können, wird ein Test, d.h. eine Entscheidungsregel nach dem folgenden Prinzip konstruiert:
- Der Stichprobenraum
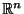 wird in zwei Borel-Mengen
wird in zwei Borel-Mengen 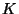 und
und
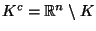 zerlegt.
zerlegt.
- Dabei heißt
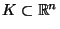 der kritische Bereich (d.h. der
Ablehnungsbereich der Nullhypothese
der kritische Bereich (d.h. der
Ablehnungsbereich der Nullhypothese 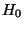 ).
).
- Die Nullhypothese
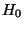 wird verworfen (d.h. abgelehnt), falls
wird verworfen (d.h. abgelehnt), falls
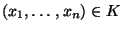 .
.
- Ansonsten, d.h. falls
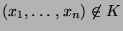 , wird
, wird 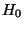 nicht verworfen.
nicht verworfen.
Mit anderen Worten:
Dies führt zu der folgenden
- Definition 5.27
 Sei
Sei
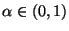 eine beliebige
(vorgegebene) Zahl. Man sagt, daß die in (70)
eingeführte Stichprobenfunktion
eine beliebige
(vorgegebene) Zahl. Man sagt, daß die in (70)
eingeführte Stichprobenfunktion
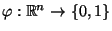 ein Test
zum Niveau
ein Test
zum Niveau 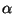 ist, falls
ist, falls
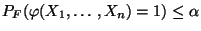 |
(71) |
für jedes
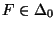 . Falls außerdem noch
. Falls außerdem noch
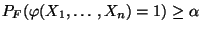 |
(72) |
für jedes
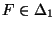 , dann heißt
, dann heißt
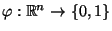 ein
unverfälschter Test zum Niveau
ein
unverfälschter Test zum Niveau 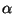 .
.
- Beachte
-
- Für jedes
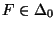 heißt
die Wahrscheinlichkeit für Fehler erster Art, und
heißt
die Wahrscheinlichkeit für Fehler erster Art, und
- für jedes
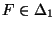 heißt
die Wahrscheinlichkeit für Fehler zweiter Art.
heißt
die Wahrscheinlichkeit für Fehler zweiter Art.
- Von besonderem Interesse sind Tests, deren Wahrscheinlichkeiten
für Fehler erster Art eine vorgegebene
,,Irrtumswahrscheinlichkeit''
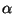 nicht überschreiten und für
die gleichzeitig die Wahrscheinlichkeiten für Fehler zweiter Art
möglichst klein sind.
nicht überschreiten und für
die gleichzeitig die Wahrscheinlichkeiten für Fehler zweiter Art
möglichst klein sind.
Falls die Familie 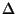 der insgesamt in Betracht gezogenen
Verteilungsfunktionen
der insgesamt in Betracht gezogenen
Verteilungsfunktionen 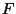 der Stichprobenvariablen
der Stichprobenvariablen  eine
parametrische Familie
eine
parametrische Familie
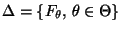 von
Verteilungsfunktionen ist, dann zerlegen wir
von
Verteilungsfunktionen ist, dann zerlegen wir 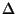 auf die
folgende Weise in zwei Teilmengen
auf die
folgende Weise in zwei Teilmengen 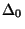 und
und 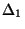 :
:
- Betrachten eine Zerlegung
des Parameterraumes
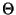 in zwei disjunkte Teilmengen
in zwei disjunkte Teilmengen
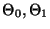 , so daß
, so daß
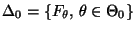
bzw.
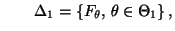
- wobei die Hypothesen
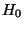 und
und 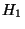 dann wie folgt formuliert
werden:
dann wie folgt formuliert
werden:
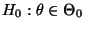
bzw.
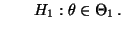
- Beispiel
 Sei
Sei 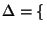 N
N
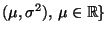 die Familie der (eindimensionalen) Normalverteilungen mit einer
vorgegebenen (bekannten) Varianz
die Familie der (eindimensionalen) Normalverteilungen mit einer
vorgegebenen (bekannten) Varianz 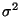 . Dann ist
. Dann ist
-
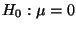 eine einfache Hypothese,
eine einfache Hypothese,
- während
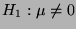 eine zusammengesetzte Hypothese ist.
eine zusammengesetzte Hypothese ist.
Für parametrische Verteilungsfamilien können die Begriffe, die in
Definition 5.27 eingeführt wurden, wie folgt spezifiziert bzw.
durch weitere Begriffe ergänzt werden.
- Definition 5.28
-
- Beachte
-
- Bei der praktischen Konstruktion des kritischen Bereichs
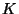 eines
Parametertest zum Niveau
eines
Parametertest zum Niveau 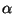 kann oft wie folgt vorgegangen
werden:
kann oft wie folgt vorgegangen
werden:
- Bestimme eine Stichprobenfunktion
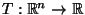 (genannt Testgröße), so daß
(genannt Testgröße), so daß
- die Zufallsvariable
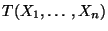 für jedes
für jedes
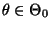 die gleiche (bekannte) Verteilung hat, und
die gleiche (bekannte) Verteilung hat, und
- bestimme einen Schwellenwert
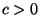 , so daß
, so daß
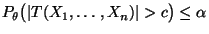 für jedes
für jedes
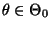 gilt.
gilt.
- Dann ist mit
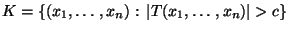 der
kritische Bereich eines Parametertests zum Niveau
der
kritische Bereich eines Parametertests zum Niveau 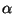 gegeben.
gegeben.
- Um einen Test zum Niveau
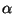 mit einer möglichst großen Macht
zu erhalten, ist es jedoch manchmal zweckmäßiger,
mit einer möglichst großen Macht
zu erhalten, ist es jedoch manchmal zweckmäßiger,
In den folgenden Abschnitten wird dieses Konstruktionsprinzip
anhand einer Reihe von Beispielen näher diskutiert.




Next: Parametertests bei Normalverteilung
Up: Tests statistischer Hypothesen
Previous: Tests statistischer Hypothesen
Contents
Roland Maier
2001-08-20
![]() die Familie der insgesamt in Betracht gezogenen (d.h.
potentiell möglichen) Verteilungsfunktionen
die Familie der insgesamt in Betracht gezogenen (d.h.
potentiell möglichen) Verteilungsfunktionen ![]() der
Stichprobenvariablen
der
Stichprobenvariablen ![]() ;
;
![]() .
.
![]() und der Alternativhypothese
und der Alternativhypothese
![]() abwägen zu können, wird ein Test, d.h. eine Entscheidungsregel nach dem folgenden Prinzip konstruiert:
abwägen zu können, wird ein Test, d.h. eine Entscheidungsregel nach dem folgenden Prinzip konstruiert:
![]() der insgesamt in Betracht gezogenen
Verteilungsfunktionen
der insgesamt in Betracht gezogenen
Verteilungsfunktionen ![]() der Stichprobenvariablen
der Stichprobenvariablen ![]() eine
parametrische Familie
eine
parametrische Familie
![]() von
Verteilungsfunktionen ist, dann zerlegen wir
von
Verteilungsfunktionen ist, dann zerlegen wir ![]() auf die
folgende Weise in zwei Teilmengen
auf die
folgende Weise in zwei Teilmengen ![]() und
und ![]() :
: