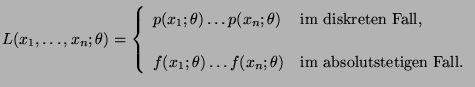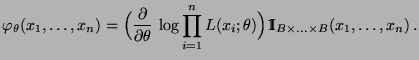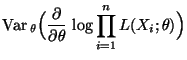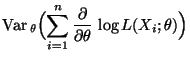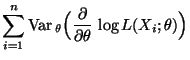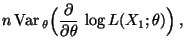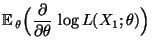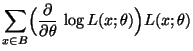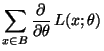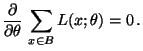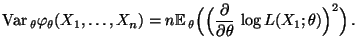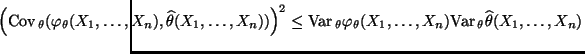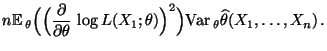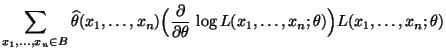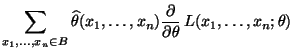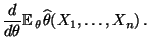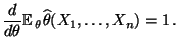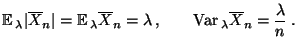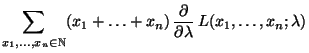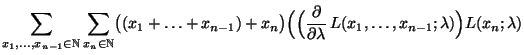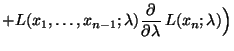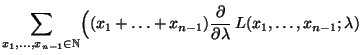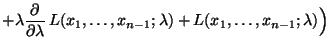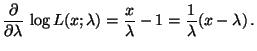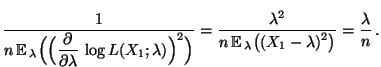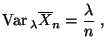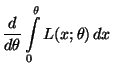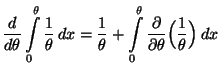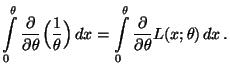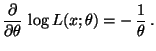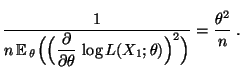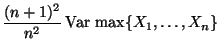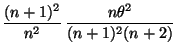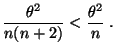Next: Suffizienz
Up: Güteeigenschaften von Punktschätzern
Previous: Erwartungstreue; mittlerer quadratischer Fehler
Contents
Ungleichung von Cramér-Rao
- In diesem Abschnitt setzen wir voraus, daß der Parameter
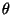 eine relle Zahl ist, d.h.,
eine relle Zahl ist, d.h.,
- es gelte
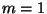 bzw.
bzw.
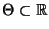 .
.
- Aus Theorem 2.1 ergibt sich, daß in der Klasse der
erwartungstreuen Schätzer die Minimierung des MQ-Fehlers
gleichbedeutend mit der Minimierung der Varianz des Schätzers ist.
- Wir werden deshalb die folgende Sprechweise verwenden.
- Definition
-
- Seien
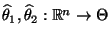 zwei
Stichprobenfunktionen, so daß für jedes
zwei
Stichprobenfunktionen, so daß für jedes
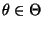 und
und
- Falls
dann sagen wir, daß der Schätzer
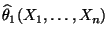 besser als der Schätzer
besser als der Schätzer
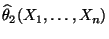 für
für 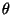 ist.
ist.
- Beispiel
 Poisson-verteilte Stichprobenvariablen
Poisson-verteilte Stichprobenvariablen
Zunächst leiten wir eine allgemeine untere Schranke für die
Varianz von Schätzern mit gewissen Regularitätseigenschaften her,
die in der Literatur Ungleichung von Cramér-Rao genannt
wird.
Das parametrische Modell
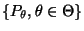 genüge den
folgenden Regularitätsbedingungen:
genüge den
folgenden Regularitätsbedingungen:
- Die Familie
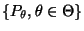 bestehe entweder nur
aus diskreten Verteilungen oder nur aus absolutstetigen
Verteilungen, wobei
bestehe entweder nur
aus diskreten Verteilungen oder nur aus absolutstetigen
Verteilungen, wobei
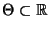 ein offenes Intervall sei.
ein offenes Intervall sei.
- Die Menge
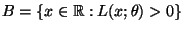 hänge nicht von
hänge nicht von
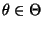 ab, wobei die Likelihood-Funktion
ab, wobei die Likelihood-Funktion
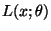 gegeben ist durch
und
gegeben ist durch
und
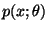 bzw.
bzw.
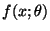 die
Wahrscheinlichkeitsfunktion bzw. Dichte von
die
Wahrscheinlichkeitsfunktion bzw. Dichte von 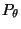 ist.
ist.
- Die Ableitung
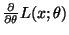 existiere für beliebige
existiere für beliebige
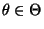 und
und 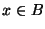 .
.
- Vertauschbarkeit von Ableitung und Summe/Integral: Für jedes
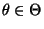 gelte
gelte
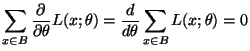 im
diskreten Fall im
diskreten Fall |
(28) |
bzw.
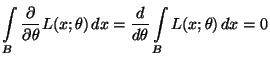 im
absolutstetigen Fall. im
absolutstetigen Fall. |
(29) |
Theorem 2.2
Sei
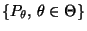
eine Familie von
Verteilungen, die den Regularitätsbedingungen
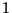
-
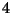
genügt, und
sei
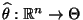
eine Stichprobenfunktion, so
daß für jedes
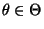
-
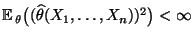 ,
,
- die Ableitung
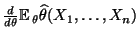 existiert und
existiert und
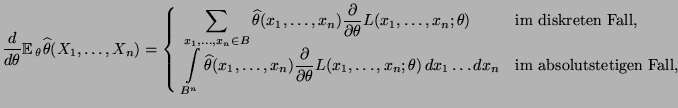 |
(30) |
wobei
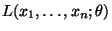 die Likelihood-Funktion ist mit
die Likelihood-Funktion ist mit
Dann gilt für jedes
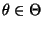
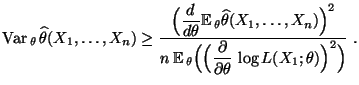 |
(31) |
- Beweis
-
- Wir betrachten zunächst den diskreten Fall.
- Für jedes
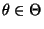 sei die Abbildung
sei die Abbildung
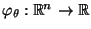 gegeben durch
gegeben durch
- Dann gilt für jedes
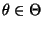
wobei sich die letzten beiden Gleichheiten aus der Unabhängigkeit
bzw. identischen Verteiltheit der Stichprobenvariablen
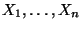 ergeben.
ergeben.
- Außerdem gilt
- Somit gilt
- Aus der Ungleichung von Cauchy-Schwarz (vgl. Theorem WR-4.11)
ergibt sich nun, daß
- Wegen
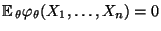 ergibt sich
andererseits, daß
ergibt sich
andererseits, daß
- Damit ist (31) für den diskreten Fall bewiesen. Im
absolutstetigen Fall verläuft der Beweis analog.

Korollar 2.1
Sei
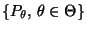
eine Familie von Verteilungen
und
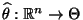
eine Stichprobenfunktion, die
den Bedingungen von Theorem
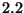
genügen. Falls
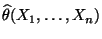
ein erwartungstreuer Schätzer für
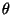
ist, dann gilt
für jedes
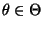
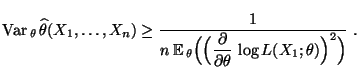 |
(32) |
- Beweis
-
- Weil
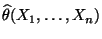 erwartungstreu ist, gilt
bzw.
erwartungstreu ist, gilt
bzw.
- Die Behauptung ergibt sich nun unmittelbar aus der
Cramér-Rao-Ungleichung (31).

- Beispiel
 Poisson-verteilte Stichprobenvariablen
(Fortsetzung)
Poisson-verteilte Stichprobenvariablen
(Fortsetzung)
- Falls
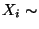 Poi
Poi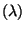 , dann gilt
, dann gilt
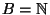 und
und
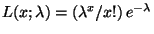 für jedes
für jedes
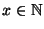 bzw.
bzw.
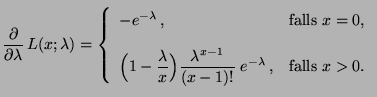 |
(33) |
- Somit gilt
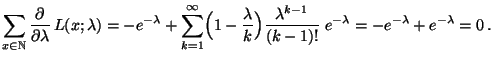 |
(34) |
- Die Regularitätsbedingungen 1-4, die unmittelbar vor
Theorem 2.2 formuliert wurden, sind also erfüllt.
- Wir zeigen nun, daß der Schätzer
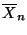 für
für 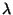 die
Bedingungen von Theorem 2.2 erfüllt.
die
Bedingungen von Theorem 2.2 erfüllt.
- Für jedes
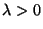 gilt
und somit
gilt
und somit
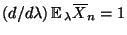 .
.
- Hieraus und aus (33) ergibt sich die Gültigkeit der
Bedingung (30) mittels vollständiger Induktion:
- Für
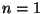 gilt
gilt
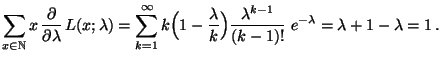 |
(35) |
- Wir nehmen nun an, daß
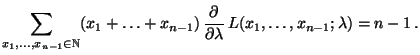 |
(36) |
- Dann gilt
- Außerdem gilt für jedes
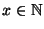
- Hieraus folgt, daß
- Weil
ist damit gezeigt, daß in der Klasse derjenigen Schätzer, die die
Bedingungen von Theorem 2.2 erfüllen, das
Stichprobenmittel
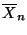 bester erwartungstreuer Schätzer
für
bester erwartungstreuer Schätzer
für 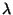 ist.
ist.
- Beachte
 Es gibt jedoch Familien
Es gibt jedoch Familien
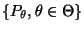 von
Verteilungen,
von
Verteilungen,
- die den Regularitätsbedingungen 1-4 nicht genügen, und
- für die man Beispiele von erwartungstreuen Schätzern konstruieren
kann, deren Varianz kleiner als die untere Schranke in
(31) ist.
- Beispiel
 Gleichverteilte Stichprobenvariablen
Gleichverteilte Stichprobenvariablen
- Sei
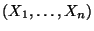 eine gleichverteilte Zufallsstichprobe mit
eine gleichverteilte Zufallsstichprobe mit
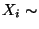 U
U
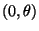 .
.
- Dann ist
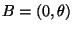 (also eine Menge, die entgegen der zweiten
Regularitätsbedingung von der spezifischen Ausprägung des
Parameters
(also eine Menge, die entgegen der zweiten
Regularitätsbedingung von der spezifischen Ausprägung des
Parameters 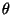 abhängt), und es gilt
abhängt), und es gilt
- Hieraus folgt, daß auch die Regularitätsbedingung
(29) nicht erfüllt ist, denn
- Außerdem gilt für jedes
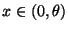
- Hieraus folgt, daß
- Wir konstruieren nun einen erwartungstreuen Schätzer für
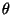 ,
dessen Varianz kleiner als
,
dessen Varianz kleiner als
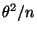 ist.
ist.
- Sei
Dann gilt (vgl. Übungsaufgabe 3.3 bzw. 6.4)
und




Next: Suffizienz
Up: Güteeigenschaften von Punktschätzern
Previous: Erwartungstreue; mittlerer quadratischer Fehler
Contents
Roland Maier
2003-03-06
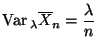 bzw.
bzw.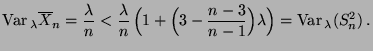
![]() genüge den
folgenden Regularitätsbedingungen:
genüge den
folgenden Regularitätsbedingungen: