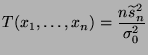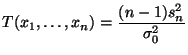- Wir nehmen an, daß
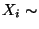 N
N
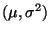 für ein (bekanntes)
für ein (bekanntes)
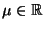 und ein (unbekanntes)
und ein (unbekanntes)
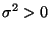 .
.
- Für einen vorgegebenen (hypothetischen) Zahlenwert
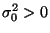 soll die Hypothese
soll die Hypothese
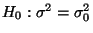 (gegen die
Alternative
(gegen die
Alternative
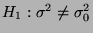 ) getestet werden, d.h.
) getestet werden, d.h.
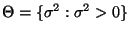 mit
mit
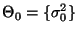 bzw.
bzw.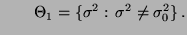
- Wir betrachten die Testgröße
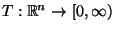 mit
mit
und die Schwellenwerte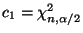 bzw.
bzw.
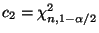 . Dabei ist
. Dabei ist
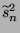 die
bereits in Abschnitt 3.2.2 eingeführte Größe
die
bereits in Abschnitt 3.2.2 eingeführte Größe
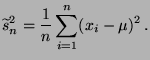
- Weil
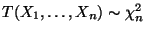 , gilt dann
, gilt dann
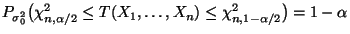 .
.
- Die Hypothese
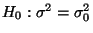 wird abgelehnt, falls
wird abgelehnt, falls
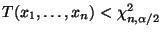 oder
oder
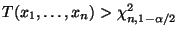 .
.
- Die Gütefunktion
![% latex2html id marker 32061
$ \alpha_n:\Theta\to[0,1]$](img2039.png) dieses Tests mit
dieses Tests mit
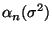
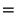
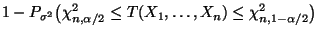
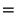
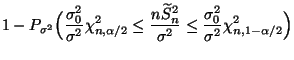
hat kein Minimum im Punkt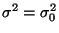 , weil die
Verteilung von
, weil die
Verteilung von
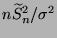 nicht von
nicht von 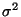 abhängt. Der Test ist also nicht unverfälscht.
abhängt. Der Test ist also nicht unverfälscht.
- Wenn jedoch beispielsweise die Hypothese
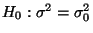 gegen die (einseitige) Alternative
gegen die (einseitige) Alternative
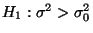 getestet werden soll, d.h.
getestet werden soll, d.h.
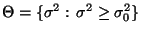 mit
dann wird der kritische Bereich
mit
dann wird der kritische Bereich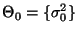 bzw.
bzw.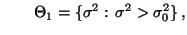
betrachtet, und die Gütefunktion![% latex2html id marker 32091
$ \alpha_n:\Theta\to[0,1]$](img2050.png) mit
mit
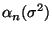
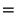
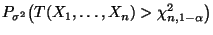
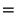
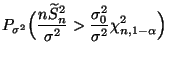
ist monoton wachsend für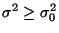 . Der einseitige
Test ist somit unverfälscht.
. Der einseitige
Test ist somit unverfälscht.
- Wegen dieser Monotonieeigenschaft ist durch den in (11)
betrachteten kritischen Bereich
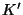 auch ein
(unverfälschter) Test zum Niveau
auch ein
(unverfälschter) Test zum Niveau 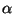 der Hypothese
der Hypothese
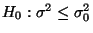 gegen die Alternativhypothese
gegen die Alternativhypothese
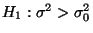 gegeben.
gegeben.
- Analog liefert der kritische Bereich
einen (unverfälschten) Test zum Niveau
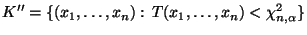
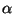 der Hypothesen
der Hypothesen
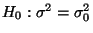 bzw.
bzw.
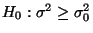 gegen
die Alternativhypothese
gegen
die Alternativhypothese
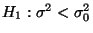 .
.
- Wir nehmen nun an, daß
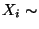 N
N
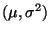 , wobei
, wobei
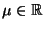 und
und
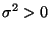 unbekannt seien.
unbekannt seien.
- Für einen vorgegebenen (hypothetischen) Zahlenwert
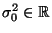 soll die Hypothese
soll die Hypothese
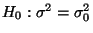 (gegen die Alternative
(gegen die Alternative
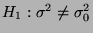 ) getestet
werden, d.h.
) getestet
werden, d.h.
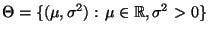 mit
mit
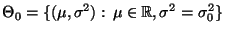 bzw.
bzw.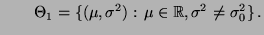
- Wir betrachten die Testgröße
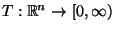 mit
mit
und die Schwellenwerte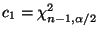 bzw.
bzw.
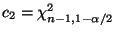 .
.
- Aus Theorem 1.11 ergibt sich, daß
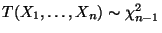 , und somit gilt
für jedes
, und somit gilt
für jedes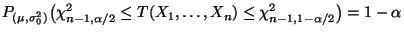
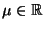 .
.
- Die Hypothese
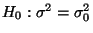 wird abgelehnt, falls
wird abgelehnt, falls
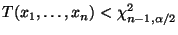 oder
oder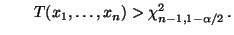
- Die Gütefunktion
![% latex2html id marker 32166
$ \alpha_n:\Theta\to[0,1]$](img2069.png) dieses Tests mit
hängt nicht von
dieses Tests mit
hängt nicht von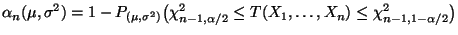
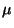 ab. Sie hat jedoch (bei fixiertem
ab. Sie hat jedoch (bei fixiertem 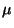 )
kein Minimum im Punkt
)
kein Minimum im Punkt
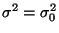 . Der Test ist also
nicht unverfälscht.
. Der Test ist also
nicht unverfälscht.
- Wenn jedoch beispielsweise die Hypothese
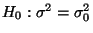 gegen die (einseitige) Alternative
gegen die (einseitige) Alternative
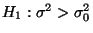 getestet werden soll, d.h.
getestet werden soll, d.h.
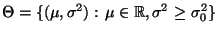 mit
dann wird der kritische Bereich
mit
dann wird der kritische Bereich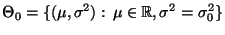 bzw.
bzw.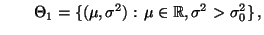
betrachtet, und die Gütefunktion![% latex2html id marker 32187
$ \alpha_n:\Theta\to[0,1]$](img2075.png) mit
mit
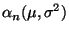
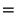
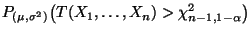
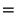
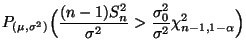
hängt nicht von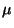 ab und ist monoton wachsend für
ab und ist monoton wachsend für
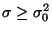 . Der einseitige Test ist somit unverfälscht.
. Der einseitige Test ist somit unverfälscht.
- Wegen dieser Monotonieeigenschaft ist durch den in
(13) betrachteten kritischen Bereich
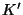 auch ein (unverfälschter) Test zum Niveau
auch ein (unverfälschter) Test zum Niveau 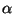 der Hypothese
der Hypothese
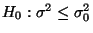 gegen die Alternativhypothese
gegen die Alternativhypothese
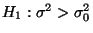 gegeben.
gegeben.
- Analog liefert der kritische Bereich
einen (unverfälschten) Test zum Niveau
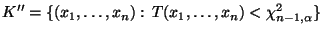
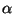 der Hypothesen
der Hypothesen
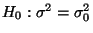 bzw.
bzw.
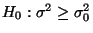 gegen
die Alternativhypothese
gegen
die Alternativhypothese
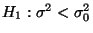 .
.