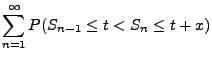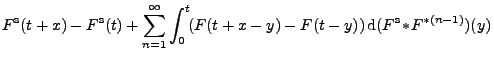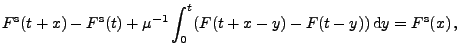Nächste Seite: Zählprozesse vom Poisson-Typ
Aufwärts: Zählprozesse; Erneuerungsprozesse
Vorherige Seite: Erneuerungsfunktion
Inhalt
Verzögerte Erneuerungprozesse; stationäre Zuwächse
Wir betrachten nun ein etwas allgemeineres Modell von
Erneuerungsprozessen. Dabei setzen wir voraus, dass
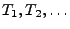 eine Folge von unabhängigen nichtnegativen
Zufallsvariablen ist und dass die Zufallsvariablen
eine Folge von unabhängigen nichtnegativen
Zufallsvariablen ist und dass die Zufallsvariablen
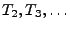 identisch verteilt sind mit der
Verteilungsfunktion
identisch verteilt sind mit der
Verteilungsfunktion 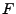 .
.
Wir lassen jedoch zu, dass 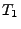 eine beliebige
Verteilungsfunktion
eine beliebige
Verteilungsfunktion 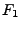 hat, die von
hat, die von 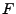 verschieden sein kann.
verschieden sein kann.
- Definition
 Die Folge
Die Folge
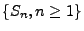 mit
mit
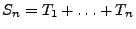 wird dann
verzögerter Erneuerungspunktprozess genannt. Der Zählprozess
wird dann
verzögerter Erneuerungspunktprozess genannt. Der Zählprozess
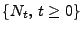 , der wiederum so wie in (1)
definiert wird, heißt verzögerter Erneuerungszählprozess
bzw. kurz verzögerter Erneuerungsprozess.
, der wiederum so wie in (1)
definiert wird, heißt verzögerter Erneuerungszählprozess
bzw. kurz verzögerter Erneuerungsprozess.
Völlig analog zu Theorem 2.4 lässt sich die folgende
Aussage beweisen.
Der Fall, wenn 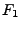 die sogenannte integrierte
Tailverteilungsfunktion
die sogenannte integrierte
Tailverteilungsfunktion 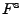 von
von 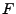 ist, ist von
besonderem Interesse, wobei
ist, ist von
besonderem Interesse, wobei
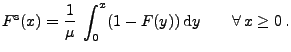 |
(19) |
Theorem 2.7
Es gelte
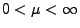
und
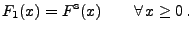 |
(20) |
Dann ist die Erneuerungsfunktion
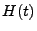
gegeben durch
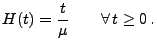 |
(21) |
- Beweis

- Wenn auf beiden Seiten der Gleichung (18) zu den
Laplace-Stieltjes-Transformierten übergegangen wird, dann ergibt
sich genauso wie im Beweis von Theorem 2.3, dass
- Weil
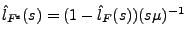 gilt, ergibt sich hieraus, dass
gilt, ergibt sich hieraus, dass
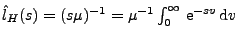 .
.
- Wegen des eineindeutigen Zusammenhanges zwischen
Erneuerungsfunktionen und Laplace-Stieltjes-Transformierten, ist
damit die Gültigkeit von (21) bewiesen.

Für verzögerte Erneuerungsprozesse
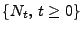 , die der
Bedingung (20) genügen, lässt sich eine wesentlich
schärfere Aussage als in Theorem 2.7 herleiten.
Hierfür benötigen wir den folgenden Begriff: Die Zufallsvariable
, die der
Bedingung (20) genügen, lässt sich eine wesentlich
schärfere Aussage als in Theorem 2.7 herleiten.
Hierfür benötigen wir den folgenden Begriff: Die Zufallsvariable
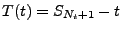 heißt Exzess zum Zeitpunkt
heißt Exzess zum Zeitpunkt  .
.
Theorem 2.8
Unter den Voraussetzungen von Theorem
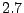
ist der
verzögerte Erneuerungsprozess
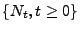
ein Prozess mit
stationären Zuwächsen.
- Beweis

- Beachte
 Weil
Weil
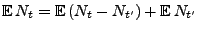 für beliebige
für beliebige
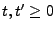 mit
mit
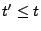 gilt, ergibt sich
unmittelbar aus Theorem 2.8, dass
gilt, ergibt sich
unmittelbar aus Theorem 2.8, dass
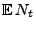 eine
lineare Funktion in
eine
lineare Funktion in 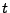 ist. Somit implizieren die
Theoreme 2.6 und 2.8 die Aussage von
Theorem 2.7.
ist. Somit implizieren die
Theoreme 2.6 und 2.8 die Aussage von
Theorem 2.7.




Nächste Seite: Zählprozesse vom Poisson-Typ
Aufwärts: Zählprozesse; Erneuerungsprozesse
Vorherige Seite: Erneuerungsfunktion
Inhalt
Ursa Pantle
2005-07-13
![]() eine Folge von unabhängigen nichtnegativen
Zufallsvariablen ist und dass die Zufallsvariablen
eine Folge von unabhängigen nichtnegativen
Zufallsvariablen ist und dass die Zufallsvariablen
![]() identisch verteilt sind mit der
Verteilungsfunktion
identisch verteilt sind mit der
Verteilungsfunktion ![]() .
.
![]() eine beliebige
Verteilungsfunktion
eine beliebige
Verteilungsfunktion ![]() hat, die von
hat, die von ![]() verschieden sein kann.
verschieden sein kann.
![]() die sogenannte integrierte
Tailverteilungsfunktion
die sogenannte integrierte
Tailverteilungsfunktion ![]() von
von ![]() ist, ist von
besonderem Interesse, wobei
ist, ist von
besonderem Interesse, wobei
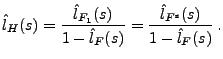
![]() , die der
Bedingung (20) genügen, lässt sich eine wesentlich
schärfere Aussage als in Theorem 2.7 herleiten.
Hierfür benötigen wir den folgenden Begriff: Die Zufallsvariable
, die der
Bedingung (20) genügen, lässt sich eine wesentlich
schärfere Aussage als in Theorem 2.7 herleiten.
Hierfür benötigen wir den folgenden Begriff: Die Zufallsvariable
![]() heißt Exzess zum Zeitpunkt
heißt Exzess zum Zeitpunkt ![]() .
.