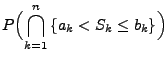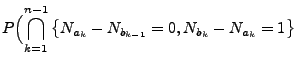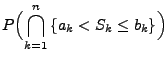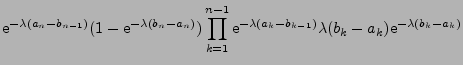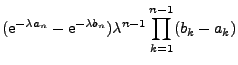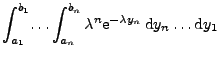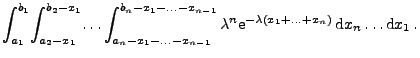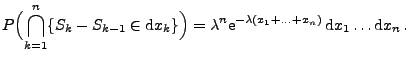Theorem 2.9
Sei
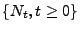
ein beliebiger Zählprozess. Dann sind die
folgenden Aussagen äquivalent:
- (a)
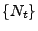 ist ein Poisson-Prozess mit Intensität
ist ein Poisson-Prozess mit Intensität
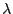 .
.
- (b)
- Für beliebige
 und
und
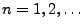 ist die Zufallsvariable
ist die Zufallsvariable
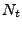 poissonverteilt mit Parameter
poissonverteilt mit Parameter 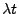 , d.h.
, d.h.
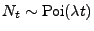 , und unter der Bedingung, dass
, und unter der Bedingung, dass
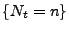 , hat
der Zufallsvektor
, hat
der Zufallsvektor
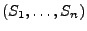 die gleiche Verteilung wie
die Ordnungsstatistik von
die gleiche Verteilung wie
die Ordnungsstatistik von 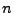 unabhängigen, in
unabhängigen, in ![$ [0,t]$](img222.png) gleichverteilten Zufallsvariablen.
gleichverteilten Zufallsvariablen.
- (c)
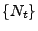 hat unabhängige Zuwächse mit
hat unabhängige Zuwächse mit
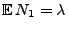 , und
für beliebige
, und
für beliebige  und
und
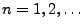 hat der Zufallsvektor
hat der Zufallsvektor
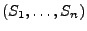 unter der Bedingung, dass
unter der Bedingung, dass
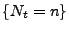 , die
gleiche Verteilung wie die Ordnungsstatistik von
, die
gleiche Verteilung wie die Ordnungsstatistik von 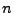 unabhängigen,
in
unabhängigen,
in ![$ [0,t]$](img222.png) gleichverteilten Zufallsvariablen.
gleichverteilten Zufallsvariablen.
- (d)
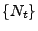 hat stationäre und unabhängige Zuwächse, und für
hat stationäre und unabhängige Zuwächse, und für
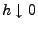 gilt
gilt
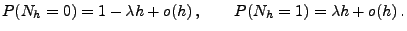 |
(24) |
- (e)
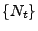 hat stationäre und unabhängige Zuwächse, und für
jedes
hat stationäre und unabhängige Zuwächse, und für
jedes  ist
ist 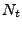 eine
eine
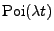 -verteilte
Zufallsvariable.
-verteilte
Zufallsvariable.
![]() mit
mit
![]() (b)
(b)
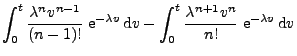
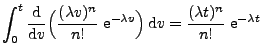
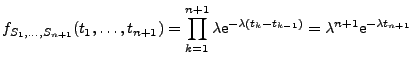
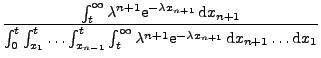
![]() (c)
(c)
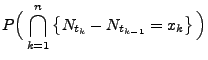
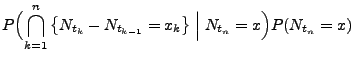
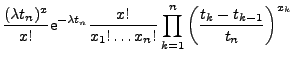
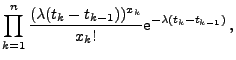
![]() (d)
(d)
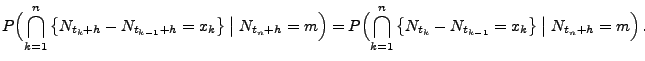
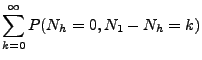
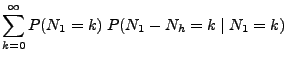
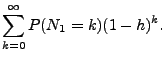
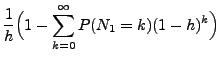
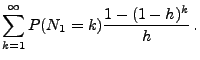
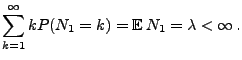
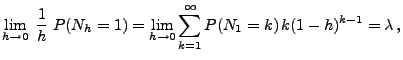
![]() (e)
(e)
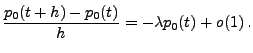
![]() (a)
(a)