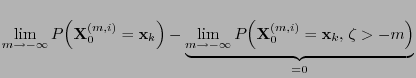Next: Monotone Coupling Algorithms
Up: Coupling Algorithms; Perfect MCMC
Previous: Coupling to the Future;
Contents
Propp-Wilson Algorithm;
Coupling from the Past
- Recall that
- the procedure of coupling to the future discussed in
Section 3.5.1 starts at a deterministic time 0
whereas the final state, i.e. the coupling time
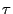 of the
simulation is random.
of the
simulation is random.
- Moreover, the state distribution of the Markov chain
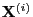 at the coupling time
at the coupling time 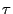 is in general not equal to the
stationary limit distribution
is in general not equal to the
stationary limit distribution
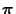 .
.
- Therefore, we will now consider a different coupling method,
- which is called Coupling from the Past (CFTP).
- It was developed in the mid 90s by Propp and Wilson at the Massachusetts Institute of Technology (MIT).
- The procedure is similar to coupling to the future (see
Section 3.5.1) but now the initial ,,time'' of the
simulation will be chosen randomly whereas the final
,,time'' is deterministic.
- In other words, the Markov chains
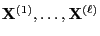 are not started at
,,time'' 0,
are not started at
,,time'' 0,
- but sufficiently far away in the ,,past'' such that by time 0 at
the latest all paths will have merged.
For the precise mathematical modeling of this procedure we need the
following notation.
- Definition
 The random variable
The random variable
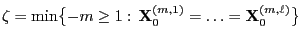 is called CFTP coupling time where we define
is called CFTP coupling time where we define
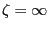 if there is no
integer
if there is no
integer 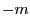 such that
such that
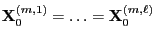 .
.
Theorem 3.23

Let
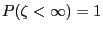
.
Then, for all
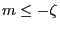
,
Moreover, for arbitrary
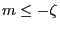
and
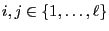
,
- Proof
-
- Remarks
-
- If the number
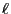 of elements in the state space
of elements in the state space
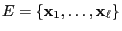 is large,
is large,
- the MCMC simulation of
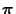 based on the CFTP algorithm by Propp
and Wilson can be computationally inefficient
based on the CFTP algorithm by Propp
and Wilson can be computationally inefficient
- as for every initial state
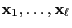 a complete
path needs to be generated.
a complete
path needs to be generated.
- However, in some cases the computational complexity can be
reduced. Examples will be discussed in Sections 3.5.3
and 3.5.4.
- In these special situations the state space
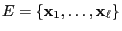 and the update function
and the update function
![$ \varphi:E\times(0,1]\to E$](img173.png) possess certain monotonicity
properties.
possess certain monotonicity
properties.
- As a consequence it suffices to consider a single sequence
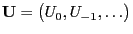 of independent and
of independent and
![$ (0,1]$](img165.png) -uniformly distributed innovations.
-uniformly distributed innovations.
- Moreover, only two different paths need to be generated.




Next: Monotone Coupling Algorithms
Up: Coupling Algorithms; Perfect MCMC
Previous: Coupling to the Future;
Contents
Ursa Pantle
2006-07-20
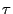 of the
simulation is random.
of the
simulation is random.
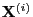 at the coupling time
at the coupling time 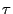 is in general not equal to the
stationary limit distribution
is in general not equal to the
stationary limit distribution
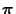 .
.
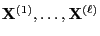 are not started at
,,time'' 0,
are not started at
,,time'' 0,