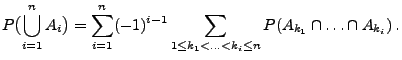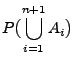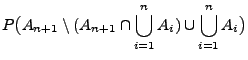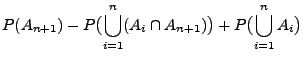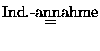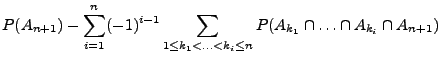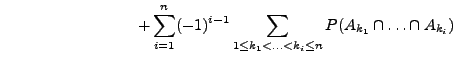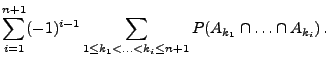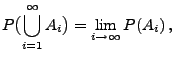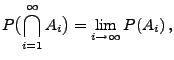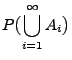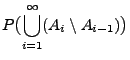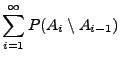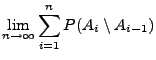- Die Mengenfunktion
![$ P:\mathcal{F}\rightarrow[0,1]$](img129.png) heißt Wahrscheinlichkeitsmaß auf
heißt Wahrscheinlichkeitsmaß auf
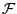 , falls
, falls
- (P1)
-
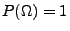 (,,Normiertheit'')
(,,Normiertheit'')
- (P2)
-
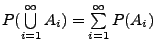 für paarweise disjunkte
für paarweise disjunkte
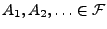 (,,
(,,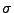 -Additivität'')
-Additivität'')
- Falls
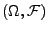 ein Messraum und
ein Messraum und 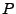 ein
Wahrscheinlichkeitsmaß auf
ein
Wahrscheinlichkeitsmaß auf
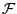 ist, dann heißt das Tripel
ist, dann heißt das Tripel
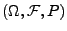 Wahrscheinlichkeitsraum.
Wahrscheinlichkeitsraum.
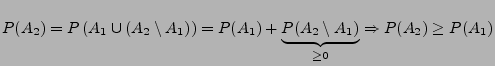
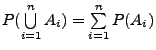 für jede endliche Folge
für jede endliche Folge
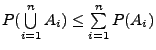 für jede beliebige Folge
für jede beliebige Folge