



Next: Einfache Urnenmodelle
Up: Endliche Wahrscheinlichkeitsräume
Previous: Endliche Wahrscheinlichkeitsräume
Contents
Laplacescher Wahrscheinlichkeitsraum
Für jedes
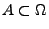 bezeichne
bezeichne 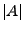 die Anzahl der
Elemente, die zu
die Anzahl der
Elemente, die zu 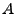 gehören. Es gelte
gehören. Es gelte
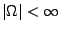 (und
damit auch
(und
damit auch
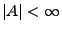 für jedes
für jedes
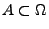 ). Ein
Wahrscheinlichkeitsraum
). Ein
Wahrscheinlichkeitsraum
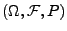 mit
mit
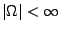 heißt endlicher Wahrscheinlichkeitsraum.
heißt endlicher Wahrscheinlichkeitsraum.
- Definition
 Ein endlicher Wahrscheinlichkeitsraum
Ein endlicher Wahrscheinlichkeitsraum
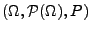 ,
bei dem alle Elementarereignisse die gleiche Wahrscheinlichkeit
haben,
d.h.,
,
bei dem alle Elementarereignisse die gleiche Wahrscheinlichkeit
haben,
d.h.,
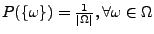 ,
heißt Laplacescher Wahrscheinlichkeitsraum.
,
heißt Laplacescher Wahrscheinlichkeitsraum.
- Beachte
 Sei
Sei
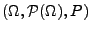 ein Laplacescher
Wahrscheinlichkeitsraum. Für jedes
ein Laplacescher
Wahrscheinlichkeitsraum. Für jedes
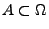 gilt dann
gilt dann
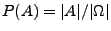 wegen der
wegen der 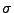 -Additivität von
Wahrscheinlichkeitsmaßen. Die so gegebene Wahrscheinlichkeit
-Additivität von
Wahrscheinlichkeitsmaßen. Die so gegebene Wahrscheinlichkeit
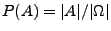 heißt Laplacesche Wahrscheinlichkeit.
heißt Laplacesche Wahrscheinlichkeit.
- Beispiel
 (zweimaliges Würfeln)
(zweimaliges Würfeln)
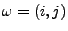
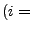 Augenzahl beim 1. Wurf;
Augenzahl beim 1. Wurf;
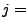 Augenzahl beim 2. Wurf)
Augenzahl beim 2. Wurf)
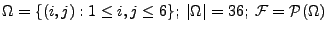 .
.
Sei
![$ p:\Omega \rightarrow [0,1]$](img233.png) mit
mit
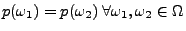 und
und
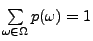 .
Hieraus folgt, dass
.
Hieraus folgt, dass
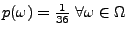 .
.
Für ein beliebiges Ereignis
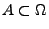 definieren wir
definieren wir
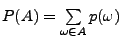 . D.h.
. D.h.
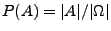 .
.
Sei beispielsweise
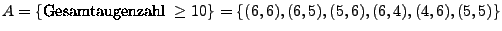 .
.
Dann gilt 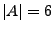 und somit
und somit
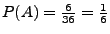 .
.
Ursa Pantle
2004-05-10
![]() bezeichne
bezeichne ![]() die Anzahl der
Elemente, die zu
die Anzahl der
Elemente, die zu ![]() gehören. Es gelte
gehören. Es gelte
![]() (und
damit auch
(und
damit auch
![]() für jedes
für jedes
![]() ). Ein
Wahrscheinlichkeitsraum
). Ein
Wahrscheinlichkeitsraum
![]() mit
mit
![]() heißt endlicher Wahrscheinlichkeitsraum.
heißt endlicher Wahrscheinlichkeitsraum.