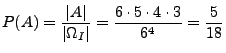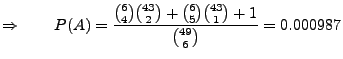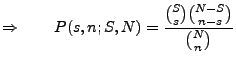Next: Geometrische Wahrscheinlichkeiten
Up: Endliche Wahrscheinlichkeitsräume
Previous: Laplacescher Wahrscheinlichkeitsraum
Contents
Einfache Urnenmodelle
Gegeben sei eine Urne mit 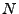 Elementen, die mit den Zahlen
Elementen, die mit den Zahlen
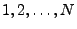 numeriert werden. Aus dieser Urne werden
numeriert werden. Aus dieser Urne werden  Elemente ,,zufällig'' entnommen. Ergebnis des gesamten
Losvorganges ist ein
Elemente ,,zufällig'' entnommen. Ergebnis des gesamten
Losvorganges ist ein  -Tupel
-Tupel
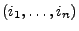 . Dabei gibt
. Dabei gibt
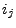 die Nummer des Elementes an, das bei der
die Nummer des Elementes an, das bei der 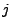 -ten Ziehung
entnommen wird. Wir betrachten vier verschiedene Arten von
Losvorgängen, die sich durch die folgenden Auswahlarten ergeben:
-ten Ziehung
entnommen wird. Wir betrachten vier verschiedene Arten von
Losvorgängen, die sich durch die folgenden Auswahlarten ergeben:
- mit Zurücklegen (d.h., Mehrfachziehungen sind möglich)
- ohne Zurücklegen (d.h., jedes Element kann maximal einmal gezogen werden)
- mit Reihenfolge (d.h.
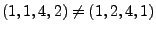 )
)
- ohne Reihenfolge (d.h.
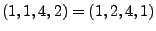 )
)
Sei
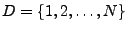 die Menge der Elemente, die sich zu
Beginn des Zufallsexperimentes in der Urne befinden. Die
Grundmengen
die Menge der Elemente, die sich zu
Beginn des Zufallsexperimentes in der Urne befinden. Die
Grundmengen 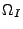 -
-
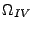 , die die vier
verschiedenen Arten von Losvorgängen modellieren, haben die
folgende Gestalt:
, die die vier
verschiedenen Arten von Losvorgängen modellieren, haben die
folgende Gestalt:
- Auswahl mit Reihenfolge und mit Zurücklegen
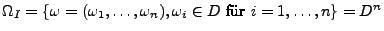
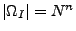
- Auswahl mit Reihenfolge und ohne Zurücklegen
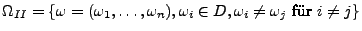
Stufe 1: 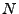 Möglichkeiten
Möglichkeiten
Stufe 2: 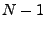 Möglichkeiten
Möglichkeiten
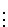
Stufe  :
: 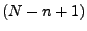 Möglichkeiten
Möglichkeiten
Also:
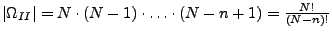
Wichtiger Spezialfall: 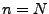 (Permutationen)
(Permutationen)
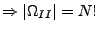
- Auswahl ohne Reihenfolge und ohne Zurücklegen
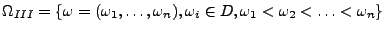
Also:
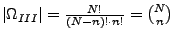 (Binomialkoeffizient)
(Binomialkoeffizient)
- Auswahl ohne Reihenfolge und mit Zurücklegen
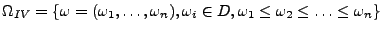
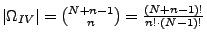
Zusammenfassung
Auswahl vom Umfang  aus aus
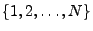 |
mit Zurücklegen |
ohne Zurücklegen |
|
| mit Reihenfolge |
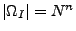 |
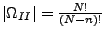 |
unterscheidbare Marken |
| ohne Reihenfolge |
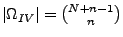 |
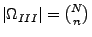 |
nicht unterscheidbare Marken |
| |
mit Mehrfachbelegung |
ohne Mehrfachbelegung |
Verteilung von  Marken auf Marken auf 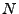 Zellen Zellen |
- Beispiele
-
- Von den 16 Mannschaften, die am UEFA-Cup eines
bestimmten Jahrganges teilnehmen, seien 2 Mannschaften aus
Deutschland. Wie groß ist die Wahrscheinlichkeit, dass
die beiden deutschen Mannschaften in der ersten Runde gegeneinander spielen?
Lösung: 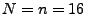 (mit Reihenfolge und ohne
Zurücklegen)
(mit Reihenfolge und ohne
Zurücklegen)
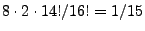 .
.
- Angenommen: 4 identische Würfel werden gleichzeitig geworfen.
Wie groß ist die Wahrscheinlichkeit, dass
die vier Augenzahlen voneinander verschieden sind?
Erste Lösungsidee:
Auswahl ohne Reihenfolge und mit Zurücklegen.
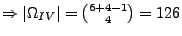 .
.
Problem: keine Chancengleichheit der Elementarereignisse,
denn
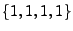 ist (4!)-mal weniger wahrscheinlich als
ist (4!)-mal weniger wahrscheinlich als
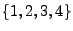 (wegen der Permutationen).
(wegen der Permutationen).
besser: Wir nehmen an, dass wir die 4 Würfel nacheinander werfen
und dabei auf die Reihenfolge der erzielten Augenzahlen achten.
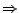 Laplacescher Wahrscheinlichkeitsraum.
Laplacescher Wahrscheinlichkeitsraum.
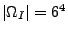 (Anzahl der möglichen Fälle),
(Anzahl der möglichen Fälle),
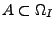 ,
,
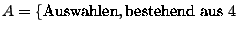 unterschiedlichen
Augenzahlen
unterschiedlichen
Augenzahlen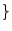 ,
,
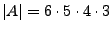 (Anzahl
der günstigen Fälle)
(Anzahl
der günstigen Fälle)
- Zahlenlotto:
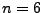 aus
aus 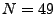 (ohne Reihenfolge und ohne Zurücklegen)
(ohne Reihenfolge und ohne Zurücklegen)
Wie groß ist die Wahrscheinlichkeit,
mindestens 4 Richtige zu haben?
Lösung:
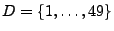 ,
,
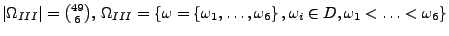
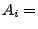 { genau
{ genau 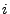 Richtige },
Richtige },
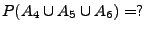
Weil
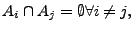 gilt
gilt
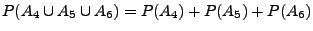 .
.
Dabei ist
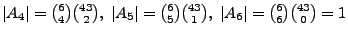 Beachte
Beachte  Dieses Beispiel ist ein Spezialfall der
hypergeometrischen Verteilung.
Dieses Beispiel ist ein Spezialfall der
hypergeometrischen Verteilung.
- Hypergeometrische Verteilung
 Betrachten
Urne mit
Betrachten
Urne mit 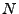 Elementen, wobei zwei Typen von Elementen vorhanden seien
(
Elementen, wobei zwei Typen von Elementen vorhanden seien
(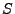 schwarze Kugeln,
schwarze Kugeln, 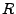 rote Kugeln);
rote Kugeln); 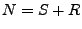 . Sei
. Sei 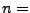 Anzahl der
insgesamt entnommenen Kugeln;
Anzahl der
insgesamt entnommenen Kugeln; 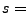 Anzahl der entnommenen schwarzen Kugeln;
Anzahl der entnommenen schwarzen Kugeln;
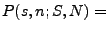 Wahrscheinlichkeit, dass
Wahrscheinlichkeit, dass
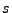 schwarze Kugeln bei der Entnahme von insgesamt
schwarze Kugeln bei der Entnahme von insgesamt  Kugeln
gezogen werden, falls
von den
Kugeln
gezogen werden, falls
von den 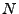 vorhandenen Kugeln
vorhandenen Kugeln 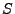 schwarz sind.
schwarz sind.




Next: Geometrische Wahrscheinlichkeiten
Up: Endliche Wahrscheinlichkeitsräume
Previous: Laplacescher Wahrscheinlichkeitsraum
Contents
Ursa Pantle
2004-05-10
![]() Elementen, die mit den Zahlen
Elementen, die mit den Zahlen
![]() numeriert werden. Aus dieser Urne werden
numeriert werden. Aus dieser Urne werden ![]() Elemente ,,zufällig'' entnommen. Ergebnis des gesamten
Losvorganges ist ein
Elemente ,,zufällig'' entnommen. Ergebnis des gesamten
Losvorganges ist ein ![]() -Tupel
-Tupel
![]() . Dabei gibt
. Dabei gibt
![]() die Nummer des Elementes an, das bei der
die Nummer des Elementes an, das bei der ![]() -ten Ziehung
entnommen wird. Wir betrachten vier verschiedene Arten von
Losvorgängen, die sich durch die folgenden Auswahlarten ergeben:
-ten Ziehung
entnommen wird. Wir betrachten vier verschiedene Arten von
Losvorgängen, die sich durch die folgenden Auswahlarten ergeben: