



Nächste Seite: Güteeigenschaften; punktweise und gleichmäßige
Aufwärts: Kolmogorow-Smirnow-Test
Vorherige Seite: Empirische Verteilungsfunktion; KS-Teststatistik
Inhalt
Asymptotische Verteilung
Wir untersuchen nun die asymptotische Verteilung der in
(2) eingeführten KS-Teststatistik
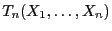 , wenn
, wenn
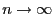 . Hierfür stellen wir
zunächst einige Hilfsmittel bereit.
. Hierfür stellen wir
zunächst einige Hilfsmittel bereit.
Insbesondere benötigen wir den folgenden Stetigkeitssatz für
charakteristische Funktionen von Zufallsvektoren, der eine
mehrdimensionale Verallgemeinerung von Theorem WR-5.20 ist und
den wir hier ohne Beweis angeben.
Lemma 5.1

Sei
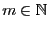
, und seien
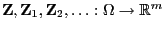
beliebige
Zufallsvektoren mit den charakteristischen Funktionen
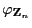
bzw
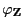
. Es gilt
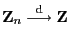
genau dann, wenn
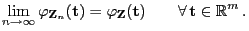 |
(4) |
Außerdem benötigen wir einen multivariaten zentralen
Grenzwertsatz für Summen von unabhängigen und identisch
verteilten Zufallsvektoren,
- dessen Beweis mit Hilfe von Lemma 5.1 auf den
entsprechenden zentralen Grenzwertsatz für reellwertige
Zufallsvariablen (vgl. Theorem WR-5.16) zurückgeführt werden
kann.
- Dieser Ansatz wird in der englischsprachigen Literatur Cramèr-Wold-Device genannt.
- Beweis
-
Der folgende Grenzwertsatz, der bereits in Abschnitt I-1.5.3
erwähnt wurde, liefert eine Näherungsformel für die
Verteilungsfunktion von
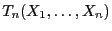 bei großem
Stichprobenumfang
bei großem
Stichprobenumfang  .
.
Theorem 5.1

Die Verteilungsfunktion
![$ F_0:\mathbb{R}\to[0,1]$](img1875.png)
sei stetig. Unter
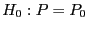
gilt dann
wobei
![$ K:\mathbb{R}\to[0,1]$](img1910.png)
die Verteilungsfunktion der sogenannten
Kolmogorow-Verteilung ist mit
![$\displaystyle K(x)=\left\{\begin{array}{ll} 1-2\sum\limits_{k=1}^\infty (-1)^{k...
...& \mbox{wenn $x>0$,}\ [3\jot] 0 , & \mbox{wenn $x\le 0$.} \end{array}\right.$](img1911.png) |
(11) |
- Beweis
-
- Wir skizzieren hier lediglich die Beweisidee, denn der komplette
Beweis von Theorem 5.1 (vgl. z.B. A. van der Vaart
und J. Wellner (1996)) geht über den Rahmen dieser Vorlesung
hinaus,
- weil er relativ tiefliegende Hilfsmittel aus der Theorie der
stochastischen Prozesse erfordert, die in den Kursvorlesungen
nicht behandelt werden.
- Dabei wird insbesondere der Begriff der Verteilungskonvergenz
in Funktionenräumen sowie ein so genannter funktionaler
zentraler Grenzwertsatz benötigt,
- der als eine (unendlich dimensionale) Verallgemeinerung der
klassischen zentralen Grenzwertsätze für Summen von rellwertigen
Zufallsvariablen (vgl. Abschnitt WR-5.3) bzw. von
endlich-dimensionalen Zufallsvektoren (vgl.
Lemma 5.2) aufgefasst werden kann.
- Weil die Verteilung von
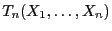 nicht von
nicht von 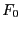 abhängt (vgl. Theorem I-1.19), können wir o.B.d.A. annehmen,
dass
abhängt (vgl. Theorem I-1.19), können wir o.B.d.A. annehmen,
dass 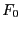 die Verteilungsfunktion der Gleichverteilung in
die Verteilungsfunktion der Gleichverteilung in
![$ [0,1]$](img1880.png) ist, d.h.,
ist, d.h., 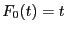 für jedes
für jedes ![$ t\in[0,1]$](img1913.png) .
.
- Für beliebige
![$ t_1,\ldots, t_m\in[0,1]$](img1916.png) gilt dann
gilt dann
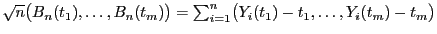 , wobei
, wobei
- Man kann sich leicht überlegen, dass die Verteilung
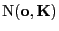 des Zufallsvektors
des Zufallsvektors
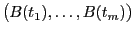 als
als
- endlich-dimensionale Verteilung des so genannten Brownschen Brückenprozesses
![$ \{B(t), t\in[0,1]\}$](img1928.png) mit
mit
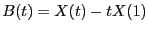 aufgefasst werden kann, wobei
aufgefasst werden kann, wobei
![$ \{X(t), t\in[0,1]\}$](img1930.png) ein (Standard-) Wiener-Prozess ist,
ein (Standard-) Wiener-Prozess ist,
- d.h.,
![$ \{X(t), t\in[0,1]\}$](img1930.png) ist ein stochastischer Prozess mit
stetigen Trajektorien und unabhängigen Zuwächsen, so dass
ist ein stochastischer Prozess mit
stetigen Trajektorien und unabhängigen Zuwächsen, so dass 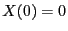 und
und
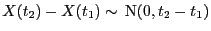 für beliebige
für beliebige
![$ t_1,t_2\in[0,1]$](img1933.png) mit
mit 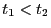 , vgl. Abschnitt 2.4 des Skriptes
zur Vorlesung ,,Wahrscheinlichkeitstheorie''.
, vgl. Abschnitt 2.4 des Skriptes
zur Vorlesung ,,Wahrscheinlichkeitstheorie''.
- Mit Hilfe der Theorie der Verteilungskonvergenz in
Funktionenräumen sowie eines entsprechenden funktionalen zentralen
Grenzwertsatzes kann man nun zeigen, dass nicht nur die
,,endlich-dimensionalen'' Konvergenzen (13) und
(14) gelten, sondern dass darüber hinaus auch
![$\displaystyle \bigl(B_n(t), t\in[0,1]\bigr)\stackrel{{\rm d}}{\longrightarrow}\bigl(B(t), t\in[0,1]\bigr)$](img1935.png) |
(15) |
bzw.
![$\displaystyle \max\limits_{t\in[0,1]} \sqrt{n}\bigl\vert\widehat F_n(t;X_1,\ldo...
...{{\rm d}}{\longrightarrow} \max\limits_{t\in[0,1]} \bigl\vert B(t)\bigr\vert .$](img1936.png) |
(16) |
- Außerdem kann man zeigen, dass die Verteilungsfunktion des
Maximums
![$ \max_{t\in[0,1]} \bigl\vert B(t)\bigr\vert$](img1937.png) der Brownschen Brücke
der Brownschen Brücke
![$ \{B(t), t\in[0,1]\}$](img1928.png) durch (11) gegeben
ist.
durch (11) gegeben
ist.

- Beachte
-




Nächste Seite: Güteeigenschaften; punktweise und gleichmäßige
Aufwärts: Kolmogorow-Smirnow-Test
Vorherige Seite: Empirische Verteilungsfunktion; KS-Teststatistik
Inhalt
Hendrik Schmidt
2006-02-27
![]() , wenn
, wenn
![]() . Hierfür stellen wir
zunächst einige Hilfsmittel bereit.
. Hierfür stellen wir
zunächst einige Hilfsmittel bereit.
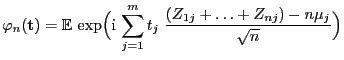
![]() bei großem
Stichprobenumfang
bei großem
Stichprobenumfang ![]() .
.
