


Next: Stationary Tessellations
Up: Random Planar Tessellations
Previous: Random Planar Tessellations
We now consider models for planar point patterns which consist of two
(or even more) different types of points,
say  and
and  . These models can be used
to analyze the spatial organization of hierarchical communication
networks. Suppose for example that we are considering the locations
of subscribers and stations respectively in a certain geographical
region. The cells handled by stations in communication networks
are often far from the regular hexagonal shape which is usually taken
as a reference model; see Lee (1993, 1995).
An alternative approach which allows one to take these
fluctuations into account is based on the idea of considering not only the
observed configuration
. These models can be used
to analyze the spatial organization of hierarchical communication
networks. Suppose for example that we are considering the locations
of subscribers and stations respectively in a certain geographical
region. The cells handled by stations in communication networks
are often far from the regular hexagonal shape which is usually taken
as a reference model; see Lee (1993, 1995).
An alternative approach which allows one to take these
fluctuations into account is based on the idea of considering not only the
observed configuration 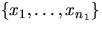 of subscribers
but also the locations
of subscribers
but also the locations  of stations as
a realization of a planar point process in a certain geographical
region; see Baccelli et al. (1996), Baccelli and
Zuyev (1997, 1998), Foss and Zuyev (1996),
Zuyev et al. (1997).
This kind of stochastic modeling is quite natural in macro-economic
studies of cellular communication systems.
of stations as
a realization of a planar point process in a certain geographical
region; see Baccelli et al. (1996), Baccelli and
Zuyev (1997, 1998), Foss and Zuyev (1996),
Zuyev et al. (1997).
This kind of stochastic modeling is quite natural in macro-economic
studies of cellular communication systems.
Assume that subscribers are served by the nearest station.
This means that
each station serves subscribers located in a certain region.
In other words, the plane is divided into convex polygonal cells,
each of which is served by a unique station (see Figure 9).
Figure 9:
Tessellation
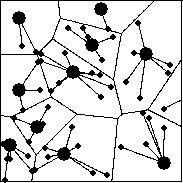 |
Such a division of the
plane is called a tessellation or mosaic if the constituent
polygons are bounded and pairwise disjoint, the union of their
closures fills the plane, and the family of polygons is locally finite,
i.e., finite on any bounded region.
In connection with the above mentioned division of the plane by a family of
spatially distributed stations, we are particularly interested in
the following kind of tessellation which is induced by a locally finite
sequence  of points in
of points in  . Let
cn denote the set of all
. Let
cn denote the set of all  for which yn is the
nearest point from
for which yn is the
nearest point from  , that is
, that is
| 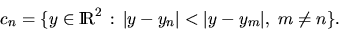 |
(1) |
The  are all
open convex polygons but some of them can be unbounded. However, if
the sequence
are all
open convex polygons but some of them can be unbounded. However, if
the sequence  is chosen in such a way that this
deficiency does not arise, then
is chosen in such a way that this
deficiency does not arise, then  constitutes
a so-called Voronoi tessellation with respect to
constitutes
a so-called Voronoi tessellation with respect to  The convex polygon cn is called the Voronoi cell with
nucleus yn; see e.g. Aurenhammer (1991),
Boots (1987), Okabe et al. (1992).
Note, however, that some authors speak of a Dirichlet
or Thiessen tessellation, instead of a Voronoi tessellation.
The convex polygon cn is called the Voronoi cell with
nucleus yn; see e.g. Aurenhammer (1991),
Boots (1987), Okabe et al. (1992).
Note, however, that some authors speak of a Dirichlet
or Thiessen tessellation, instead of a Voronoi tessellation.
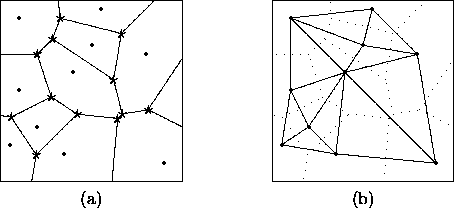
Assume that  is a Voronoi tessellation such that
every node
is a Voronoi tessellation such that
every node  is touched by exactly three cells, as in
Figure 10(a). Then a further
tessellation can be considered, the so-called
Delaunay tessellation which is constructed by linking all those
pairs from
is touched by exactly three cells, as in
Figure 10(a). Then a further
tessellation can be considered, the so-called
Delaunay tessellation which is constructed by linking all those
pairs from  which belong to neighboring
cells of the Voronoi tessellation. These links, i.e., the edges of the
Delaunay tessellation,
can model cables connecting the neighboring
stations located at the points
which belong to neighboring
cells of the Voronoi tessellation. These links, i.e., the edges of the
Delaunay tessellation,
can model cables connecting the neighboring
stations located at the points  In Figure 10(b) a realization of a Delaunay tessellation is given,
where the solid lines are the links which connect the neighboring stations.
In Figure 10(b) a realization of a Delaunay tessellation is given,
where the solid lines are the links which connect the neighboring stations.
Figure 10:
Construction of a Delaunay tesselation
 |



Next: Stationary Tessellations
Up: Random Planar Tessellations
Previous: Random Planar Tessellations
Andreas Frey
7/8/1998

![]() of points in
of points in ![]() . Let
cn denote the set of all
. Let
cn denote the set of all ![]() for which yn is the
nearest point from
for which yn is the
nearest point from ![]() , that is
, that is
![]() is a Voronoi tessellation such that
every node
is a Voronoi tessellation such that
every node ![]() is touched by exactly three cells, as in
Figure 10(a). Then a further
tessellation can be considered, the so-called
Delaunay tessellation which is constructed by linking all those
pairs from
is touched by exactly three cells, as in
Figure 10(a). Then a further
tessellation can be considered, the so-called
Delaunay tessellation which is constructed by linking all those
pairs from ![]() which belong to neighboring
cells of the Voronoi tessellation. These links, i.e., the edges of the
Delaunay tessellation,
can model cables connecting the neighboring
stations located at the points
which belong to neighboring
cells of the Voronoi tessellation. These links, i.e., the edges of the
Delaunay tessellation,
can model cables connecting the neighboring
stations located at the points ![]() In Figure 10(b) a realization of a Delaunay tessellation is given,
where the solid lines are the links which connect the neighboring stations.
In Figure 10(b) a realization of a Delaunay tessellation is given,
where the solid lines are the links which connect the neighboring stations.