Optimization of Network Architecture

 In Aalto et al. (1996) a spatial (Delaunay) tessellation model for cost optimization in large cellular communication networks has been considered, where the traffic is modelled by a fractional Brownian motion; see also Norros (1995). In Baccelli and Zuyev (1998) the following example of a parametric cost optimization has been discussed. Consider the hierarchical point process model introduced in Section 5.4 and assume that there are three hierarchy levels, i.e., k=2. A possible interpretation of the Poisson processes X⁽⁰⁾, X⁽¹⁾, X⁽²⁾ with intensities $\lambda_0$, $\lambda_1$, $\lambda_2$ is that of representing subscribers, distribution points and concentrators respectively. Suppose that the intensities $\lambda_0$ and $\lambda_2$ of subscribers and concentrators are given. The goal is to determine a value for the intensity $\lambda_1$ of distribution points such that a certain cost function becomes minimal.

Let C_x⁽ⁱ⁾ denote the Voronoi cell with nucleus at x corresponding to the point process $\{x,X_1^{(i)},X_2^{(i)},\ldots\}$.Furthermore, let X⁽⁰⁾(C_x⁽¹⁾) be the number of points from $\{X_1^{(0)},X_2^{(0)},\ldots\}$ in the Voronoi cell C_x⁽¹⁾. Set

where $a_1,\, a_{ij},\, b_{ij},\, \alpha_{ij},\, \beta_{ij} \geq 0$are some constants. Here a₁ is interpreted as the cost of a distribution point itself, $a_{i,i+1}r^{\alpha_{i,i+1}}$ is the (wiring) cost for connecting a point of level i to the closest point of level i+1 provided that the distance to this point is r. Analogously, $b_{i,i+1}r^{\beta_{i,i+1}}$ is the corresponding infrastructure cost of civil engineering.

Intuitively speaking, by increasing the intensity $\lambda_1$ of distribution points one achieves a grouping gain since less infrastructure is needed then: the cables from a distribution point to a concentrator share the same facilities. On the other hand, the wiring costs become larger.

Baccelli and Zuyev (1998) showed that the cost function $f(\lambda_1)$ introduced above can be represented in the form $f(\lambda_1) = h_1 \lambda_1 + h_2 + h_3 \lambda_1^{-\beta_{01}/2} + h_4 \lambda_1^{-\alpha_{01}/2}$,where

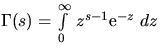where $\Gamma(s)=\int\limits_0^{\infty} \, z^{s-1} \mbox{e}^{-z}\;dz$ denotes the Euler-Gamma function. Thus, the cost function $f(\lambda_1)$ attains a unique minimum at the point $\lambda_1^{\star}$which solves the equation $h_3 \beta_{01} \lambda_1^{-\left(\beta_{01}/2+1\right)} + h_4 \alpha_{01} \lambda_1^{-\left( \alpha_{01}/2+1\right)} = 2h_1$.In particular, if $\beta_{01} = \alpha_{01} = \alpha$ then

$$\lambda_1^{\star} \, = \, \left( \frac{\alpha (h_3 + h_4)}{2h_1} \right)^{\frac{2}{2+\alpha}}.$$

Suppose now that no analytical representation formula of the cost function $f(\lambda_1)$ is available. However, assume that $f(\lambda_1)$ is the expectation $f(\lambda_1) = \Exp F\left( X^{(0)},X^{(1)},X^{(2)} \right)$of a local statistic $F\left( X^{(0)},X^{(1)},X^{(2)} \right)$, where the statistic $F\left( X^{(0)},X^{(1)},X^{(2)} \right)$ is called local if for almost every realization (x⁽⁰⁾,x⁽¹⁾,x⁽²⁾) of (X⁽⁰⁾,X⁽¹⁾,X⁽²⁾), the value of $F\left( x^{(0)},x^{(1)},x^{(2)} \right)$ depends only on those points of x⁽⁰⁾, x⁽¹⁾, x⁽²⁾ which fall in a certain compact set B(x⁽⁰⁾,x⁽¹⁾,x⁽²⁾). Furthermore, in many cases of practical interest, the function $f(\lambda_1)$ is differentiable, and the derivative can be given in the form

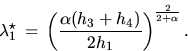
This representation formula can be used to get an estimator for $\frac{d}{d\lambda_1} f(\lambda_1)$ by estimating the expectation on the right-hand side of the last equation. The approach via such a rare perturbation estimator has been used, for instance, in Baccelli et al. (1995), and Zuyev et al. (1997) to determine a value of $\lambda_1$ such that $f(\lambda_1)$ becomes minimal.

In Section 5.1 we assumed that the association of subscribers to stations is purely distance-based. However, besides this nearest-neighbor principle, there are still other factors which can influence the division of the plane by the stations; see e.g. Lee (1995). In building stochastic models one could take this into account by considering division rules which are more general than the Voronoi tessellation.

Examples of more general tessellations are the multiplicatively weighted tessellation, the Johnson-Mehl tessellation, and the power tessellation; see Okabe et al. (1992), Møller (1992), Zuyev (1994), Aurenhammer (1987, 1991). Scheike (1994).