


Next: Stationary Marked Point Processes
Up: Homogeneous Poisson Processes
Previous: Statistical Analysis
Suppose that we want to simulate a homogeneous Poisson process with intensity
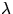 in the bounded region B where
in the bounded region B where 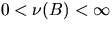 . In achieving
this goal we can use the conditional uniformity property (2.1).
Thus, we condition on the total number of points X(B) in the set B.
The simulation therefore consists of two steps. First, the Poisson
distributed random variable X(B) is simulated. If this is done, say
with the result X(B)=n, then the second step follows easily
by using (2.1), if one knows how to simulate n
independent and uniformly distributed points in the region B.
Note that it is straightforward to simulate n independent random
points uniformly distributed in [0,1]2: if
. In achieving
this goal we can use the conditional uniformity property (2.1).
Thus, we condition on the total number of points X(B) in the set B.
The simulation therefore consists of two steps. First, the Poisson
distributed random variable X(B) is simulated. If this is done, say
with the result X(B)=n, then the second step follows easily
by using (2.1), if one knows how to simulate n
independent and uniformly distributed points in the region B.
Note that it is straightforward to simulate n independent random
points uniformly distributed in [0,1]2: if 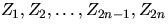 is a sequence of independent random numbers
uniformly distributed in [0,1], then the n random points
is a sequence of independent random numbers
uniformly distributed in [0,1], then the n random points
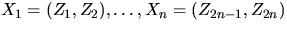 are independent
and uniformly distributed in [0,1]2. Next, translation and
scaling can be used to generate a sequence of n independent
random points uniformly distributed in an arbitrary fixed rectangle.
Now, in order to simulate n independent random points uniformly
distributed in a more complex bounded region B we can apply
different methods. One is to consider a rectangle
are independent
and uniformly distributed in [0,1]2. Next, translation and
scaling can be used to generate a sequence of n independent
random points uniformly distributed in an arbitrary fixed rectangle.
Now, in order to simulate n independent random points uniformly
distributed in a more complex bounded region B we can apply
different methods. One is to consider a rectangle 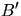 which contains B and to generate so many points in
which contains B and to generate so many points in 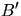 until n of them fall in B. These n random points are then
independent and uniformly distributed in B.
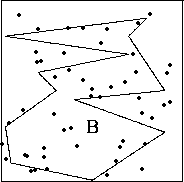
In Figure 5 this method is used to simulate n=28
random points uniformly distributed in the region B.
until n of them fall in B. These n random points are then
independent and uniformly distributed in B.
In Figure 5 this method is used to simulate n=28
random points uniformly distributed in the region B.
Figure 5:
Simulation
 |
Another way is to
approximate B by a finite number of disjoint rectangles 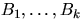 and to simulate n independent and uniformly distributed
points in the union
and to simulate n independent and uniformly distributed
points in the union 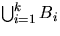 . This is realized
by choosing one of these k rectangles with probability
proportional to its area, simulating a random point uniformly distributed
in this rectangle, and repeating this procedure n times. If the
boundary of B is rather rough, it can be useful to combine the
above described methods.
. This is realized
by choosing one of these k rectangles with probability
proportional to its area, simulating a random point uniformly distributed
in this rectangle, and repeating this procedure n times. If the
boundary of B is rather rough, it can be useful to combine the
above described methods.



Next: Stationary Marked Point Processes
Up: Homogeneous Poisson Processes
Previous: Statistical Analysis
Andreas Frey
7/8/1998
