Next: Weitere Beispiele
Up: Zufallsvektoren
Previous: Definition
Contents
Eigenschaften multivariater Verteilungsfunktionen
- Asymptotisches Verhalten im Unendlichen:
 Für beliebige
Für beliebige
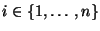 und
und
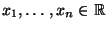 gilt
gilt
(i)
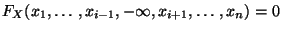 ,
wobei
(ii)
,
wobei
(ii)
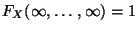 , wobei
, wobei
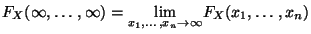 ;
;
(iii)
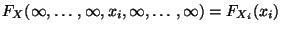 ,
wobei
,
wobei
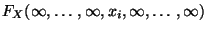 analog zu den in (i)-(ii) betrachteten Grenzwerten
definiert wird und
analog zu den in (i)-(ii) betrachteten Grenzwerten
definiert wird und
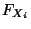 Randverteilungsfunktion von
Randverteilungsfunktion von  genannt wird.
genannt wird.
- Monotonie:

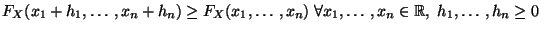
- Rechtsstetigkeit:

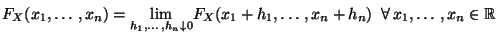
- Definition 3.8
-
- Der Zufallsvektor
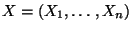 heißt diskret, falls es
eine abzählbare Menge
heißt diskret, falls es
eine abzählbare Menge
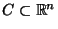 gibt, so daß
gibt, so daß
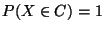 .
.
- Sei
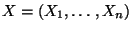 ein diskreter Zufallsvektor.
Dann heißt
ein diskreter Zufallsvektor.
Dann heißt
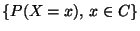 Wahrscheinlichkeitsfunktion von
Wahrscheinlichkeitsfunktion von  .
.
- Beachte
 Falls
Falls
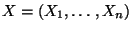 ein diskreter Zufallsvektor ist, dann sind
auch seine Komponenten
ein diskreter Zufallsvektor ist, dann sind
auch seine Komponenten
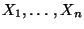 diskrete Zufallsvariablen.
Für die Wahrscheinlichkeitsfunktion
diskrete Zufallsvariablen.
Für die Wahrscheinlichkeitsfunktion
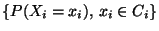 von
von  gilt
gilt
- Definition 3.9
 Der Zufallsvektor
Der Zufallsvektor
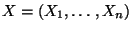 heißt absolutstetig,
falls es eine (integrierbare) Funktion
heißt absolutstetig,
falls es eine (integrierbare) Funktion
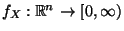 gibt, so daß
gibt, so daß
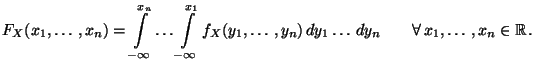 |
(10) |
Die Funktion 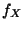 heißt (gemeinsame) Dichte von
heißt (gemeinsame) Dichte von  .
.
- Beachte
 Falls
Falls
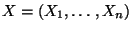 ein absolutstetiger Zufallsvektor
mit der Dichte
ein absolutstetiger Zufallsvektor
mit der Dichte 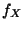 ist, dann sind
auch seine Komponenten
ist, dann sind
auch seine Komponenten
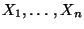 absolutstetige Zufallsvariablen.
Für die Dichte
absolutstetige Zufallsvariablen.
Für die Dichte
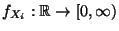 von
von  gilt
gilt
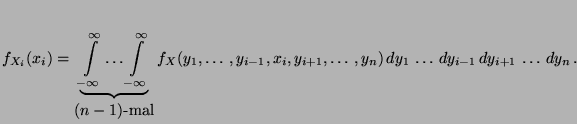 |
(11) |
- Definition 3.10
 Die in (11) betrachtete Funktion
Die in (11) betrachtete Funktion 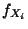 heißt
Randdichte von
heißt
Randdichte von  .
.




Next: Weitere Beispiele
Up: Zufallsvektoren
Previous: Definition
Contents
Roland Maier
2001-08-20