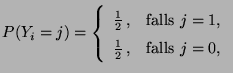Next: Linearer Zusammenhang von Zufallsvariablen
Up: Gemischte Momente
Previous: Gemischte Momente
Contents
Multiplikationsformel und Kovarianz
- Beachte
-
- Seien
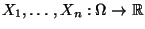 beliebige Zufallsvariable mit
beliebige Zufallsvariable mit
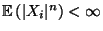 für
jedes
für
jedes
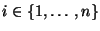 .
.
- Man kann zeigen, daß dann
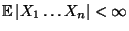 .
.
- Der Erwartungswert
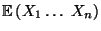 des
Produktes
des
Produktes
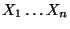 heißt gemischtes Moment der Zufallsvariablen
heißt gemischtes Moment der Zufallsvariablen
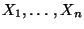 .
.
Zunächst diskutieren wir die folgende Multiplikationsformel
für den Erwartungswert des Produktes von  unabhängigen
Zufallsvariablen.
unabhängigen
Zufallsvariablen.
- Theorem 4.7
 Seien
Seien
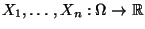 beliebige Zufallsvariable mit
beliebige Zufallsvariable mit
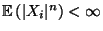 für
jedes
für
jedes
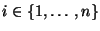 . Falls
. Falls
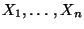 unabhängig sind, dann gilt
unabhängig sind, dann gilt
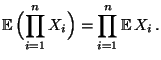 |
(19) |
- Beweis
-
- Korollar 4.8
 Seien
Seien
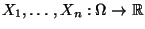 unabhängige Zufallsvariable mit
unabhängige Zufallsvariable mit
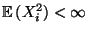 für
jedes
für
jedes
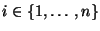 . Dann gilt
. Dann gilt
- Beweis

- Wir zeigen die Gültigkeit von
(20) zunächst für den Fall
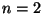 .
.
- Aus (15),
(16) und (19) ergibt sich,
daß
- Für beliebiges
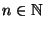 ergibt sich die Gültigkeit
von (20) mittels vollständiger Induktion.
ergibt sich die Gültigkeit
von (20) mittels vollständiger Induktion.
Wir diskutieren nun Eigenschaften des gemischten Momentes
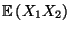 von zwei beliebigen (nicht notwendig unabhängigen)
Zufallsvariablen
von zwei beliebigen (nicht notwendig unabhängigen)
Zufallsvariablen 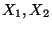 .
.
In diesem Zusammenhang führen wir zunächst die Begriffe der Kovarianz und
des Korrelationskoeffizienten ein.
- Definition 4.9
 Seien
Seien 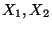 beliebige Zufallsvariable mit
beliebige Zufallsvariable mit
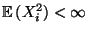 für
für 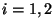 .
.
- Beachte
-
- Es ist klar, daß Kovarianz und
Korrelationskoeffizient die folgende Symmetrieeigenschaft
besitzt:
Cov 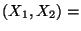 Cov Cov 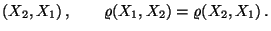 |
(22) |
- Außerdem gilt
Cov 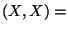 Var Var 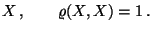 |
(23) |
Darüber hinaus gelten weitere nützliche Rechenregeln und Abschätzungen
für Kovarianz bzw. Korrelationskoeffizient.
- Theorem 4.10
 Seien
Seien 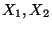 beliebige Zufallsvariable mit
beliebige Zufallsvariable mit
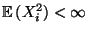 für
für 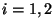 . Dann gilt
. Dann gilt
Cov 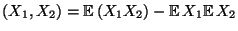 |
(24) |
und für beliebige Zahlen
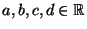
Cov 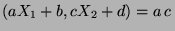 Cov Cov 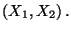 |
(25) |
Außerdem gilt die Cauchy-Schwarzsche Ungleichung
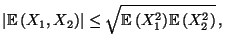 |
(26) |
und
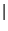 Cov Cov 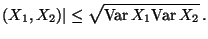 |
(27) |
- Beweis
-
- Korollar 4.11
-
- Falls
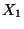 und
und 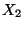 unabhängig sind, dann gilt
unabhängig sind, dann gilt
Cov 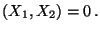 |
(28) |
d.h., 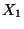 und
und 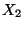 sind unkorreliert.
sind unkorreliert.
- Falls
Var
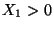 und
Var
und
Var 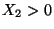 , dann gilt
, dann gilt
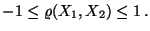 |
(29) |
- Beweis
-
- Aus (19) und (24) ergibt sich
unmittelbar die Gültigkeit von (28).
- Aus (27) und aus der Definitionsgleichung
(21) des Korrelationskoeffizienten ergeben sich
die Ungleichungen in (29).
- Beachte
 Die Aussage 1 in Korollar 4.11 läßt sich nicht umkehren, denn aus der Unkorreliertheit zweier
Zufallsvariablen
Die Aussage 1 in Korollar 4.11 läßt sich nicht umkehren, denn aus der Unkorreliertheit zweier
Zufallsvariablen 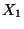 und
und 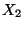 folgt im allgemeinen nicht, daß
folgt im allgemeinen nicht, daß
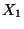 und
und 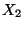 unabhängig sind.
unabhängig sind.
- Beispiel
 (zweimaliger Münzwurf)
(zweimaliger Münzwurf)




Next: Linearer Zusammenhang von Zufallsvariablen
Up: Gemischte Momente
Previous: Gemischte Momente
Contents
Roland Maier
2001-08-20
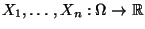 beliebige Zufallsvariable mit
beliebige Zufallsvariable mit
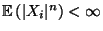 für
jedes
für
jedes
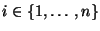 .
.
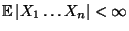 .
.
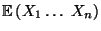 des
Produktes
des
Produktes
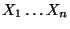 heißt gemischtes Moment der Zufallsvariablen
heißt gemischtes Moment der Zufallsvariablen
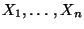 .
.
![]() unabhängigen
Zufallsvariablen.
unabhängigen
Zufallsvariablen.
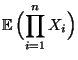
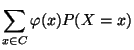
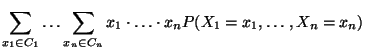
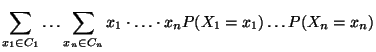
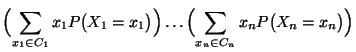
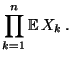
![]() von zwei beliebigen (nicht notwendig unabhängigen)
Zufallsvariablen
von zwei beliebigen (nicht notwendig unabhängigen)
Zufallsvariablen ![]() .
.