



Next: Wahrscheinlichkeitsmaße
Up: Ereignisse und Wahrscheinlichkeiten
Previous: Ereignisse als Mengen
Contents
Ereignissysteme
Aus gegebenen Ereignissen
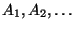 kann man durch deren
,,Verknüpfung'' weitere Ereignisse bilden. Dies wird durch die
folgenden Mengenoperationen modelliert.
kann man durch deren
,,Verknüpfung'' weitere Ereignisse bilden. Dies wird durch die
folgenden Mengenoperationen modelliert.
- Definition 2.3
-
- Vereinigungsmenge

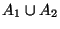 : Menge aller Elemente, die zu
: Menge aller Elemente, die zu
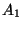 oder
oder 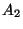 gehören.
gehören.
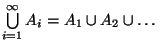 : Menge
aller Elemente, die zu mindestens einer der Mengen
: Menge
aller Elemente, die zu mindestens einer der Mengen 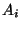 gehören.
gehören.
- Schnittmenge
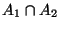 : Menge aller Elemente, die zu
: Menge aller Elemente, die zu 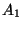 und
und 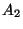 gehören.
gehören.
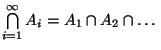 : Menge
aller Elemente, die zu jeder der Mengen
: Menge
aller Elemente, die zu jeder der Mengen 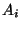 gehören.
gehören.
- Differenzmenge
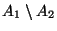 : Menge aller Elemente
von
: Menge aller Elemente
von 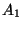 , die nicht zu
, die nicht zu 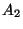 gehören.
gehören.
Spezialfall:
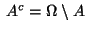 ( Komplement)
( Komplement)
- Beispiel
 Sei
Sei
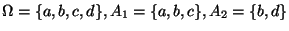 .
.
Dann gilt
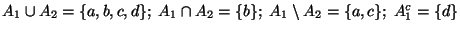 .
.
- Beachte
-
- Das Ereignis
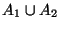 tritt genau dann ein, wenn
tritt genau dann ein, wenn 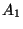 oder
oder 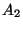 oder beide eintreten.
oder beide eintreten.
- Das Ereignis
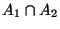 tritt genau dann ein, wenn
tritt genau dann ein, wenn 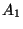 und
und 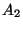 eintreten.
eintreten.
- Das Ereignis
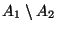 tritt genau dann ein, wenn
tritt genau dann ein, wenn 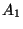 eintritt und
eintritt und 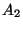 nicht eintritt.
nicht eintritt.
- Lemma 2.4
 Für beliebige Mengen
Für beliebige Mengen
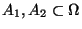 gilt:
gilt:
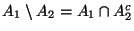 .
.
- Beweis
 klar
klar
- Definition 2.5
 Die Mengen
Die Mengen
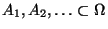 heißen
paarweise disjunkt, falls
heißen
paarweise disjunkt, falls
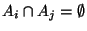 für beliebige
für beliebige
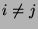 .
.
- Bemerkung
 Jede beliebige Folge von Mengen
Jede beliebige Folge von Mengen
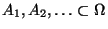 kann man in eine Folge
von paarweise disjunkten Mengen
kann man in eine Folge
von paarweise disjunkten Mengen
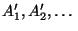 überführen:
Sei
überführen:
Sei
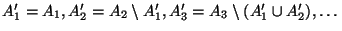
Dann gilt:
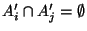 für
für 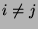 , und
, und
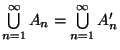
- Weitere Eigenschaften
 Sei
Sei
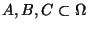 .
.
- Eindeutigkeitsgesetze:

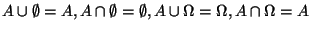
(allgemein: falls
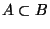 , dann gilt
, dann gilt
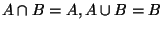 )
)
- de Morgansche Gesetze:

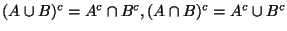
- Assoziativ-Gesetze:

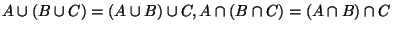
- Distributiv-Gesetze:

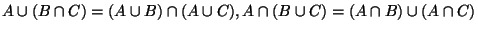
Es ist oft nicht zweckmäßig, alle möglichen Teilmengen von
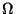 in die Modellierung einzubeziehen, sondern man betrachtet
nur die Familie derjenigen Teilmengen von
in die Modellierung einzubeziehen, sondern man betrachtet
nur die Familie derjenigen Teilmengen von 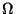 , deren
Wahrscheinlichkeiten tatsächlich von Interesse sind. Diese
Mengenfamilie soll jedoch abgeschlossen sein bezüglich der
Operationen
, deren
Wahrscheinlichkeiten tatsächlich von Interesse sind. Diese
Mengenfamilie soll jedoch abgeschlossen sein bezüglich der
Operationen
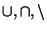 , was durch die folgende
Begriffsbildung erreicht wird.
, was durch die folgende
Begriffsbildung erreicht wird.
- Definition 2.6
 Eine nichtleere Familie
Eine nichtleere Familie
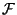 von Teilmengen
von
von Teilmengen
von 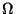 heißt Algebra, falls
heißt Algebra, falls
- (A1)
-
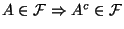
- (A2)
-
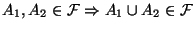
- Beispiel

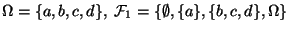 ist eine Algebra,
ist eine Algebra,
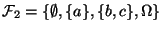 ist dagegen keine Algebra.
ist dagegen keine Algebra.
- Lemma 2.7
 Sei
Sei
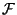 eine Algebra
und
eine Algebra
und
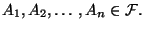 Dann gilt
Dann gilt
-
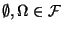
-
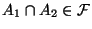
-
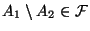
-
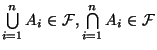
- Beweis
-
- Weil
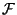 nicht leer, gibt es ein
nicht leer, gibt es ein
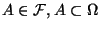 .
Also gilt
.
Also gilt
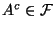 wegen (A1) bzw.
wegen (A1) bzw.
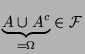 wegen (A2) bzw.
wegen (A2) bzw.
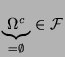 wegen (A1)
wegen (A1)
-
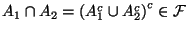
-
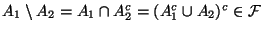
- Induktion
Um Grenzwerte bilden zu können, ist es erforderlich, daß das
Mengensystem
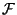 nicht nur abgeschlossen ist bezüglich
Vereinigung bzw. Durchschnitt von endlich vielen Mengen
(vgl. Teilaussage 4 von Lemma 2.7), sondern auch bezüglich
Vereinigung bzw. Durchschnitt von abzählbar unendlich
vielen Mengen. Dies wird durch die Hinzunahme der folgenden
Bedingung erreicht.
nicht nur abgeschlossen ist bezüglich
Vereinigung bzw. Durchschnitt von endlich vielen Mengen
(vgl. Teilaussage 4 von Lemma 2.7), sondern auch bezüglich
Vereinigung bzw. Durchschnitt von abzählbar unendlich
vielen Mengen. Dies wird durch die Hinzunahme der folgenden
Bedingung erreicht.
- Definition 2.8
 Eine Algebra
Eine Algebra
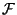 heißt
heißt 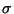 -Algebra, falls zusätzlich
-Algebra, falls zusätzlich
- (A3)

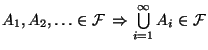 gilt.
gilt.
- Beachte
-
- Das Paar
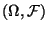 heißt Meßraum, falls
heißt Meßraum, falls
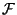 eine
eine 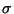 -Algebra ist.
-Algebra ist.
- Sei
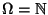 , und sei
, und sei
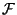 die Familie
derjenigen Teilmengen
die Familie
derjenigen Teilmengen 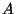 von
von
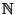 , so daß entweder
, so daß entweder 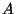 oder
oder 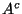 nur endlich viele Elemente hat. Das
Mengensystem
nur endlich viele Elemente hat. Das
Mengensystem
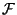 ist eine Algebra, jedoch keine
ist eine Algebra, jedoch keine
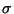 -Algebra.
-Algebra.
- Für jedes
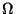 ist die Potenzmenge
ist die Potenzmenge
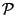 , d.h. die Familie
aller Teilmengen von
, d.h. die Familie
aller Teilmengen von 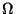 , stets eine
, stets eine 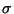 -Algebra.
-Algebra.
- Falls
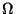 endlich oder abzählbar unendlich ist, kann
endlich oder abzählbar unendlich ist, kann
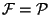 gewählt werden. Falls
gewählt werden. Falls 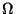 nicht abzählbar ist (z.B.
nicht abzählbar ist (z.B.
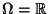 oder
oder
![$ \Omega =[0,1]),$](img103.png) dann muß eine kleinere
dann muß eine kleinere 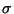 -Algebra betrachtet
werden (nicht
-Algebra betrachtet
werden (nicht
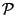 ), vgl. Abschnitt
3.1.
), vgl. Abschnitt
3.1.




Next: Wahrscheinlichkeitsmaße
Up: Ereignisse und Wahrscheinlichkeiten
Previous: Ereignisse als Mengen
Contents
Roland Maier
2001-08-20
![]() kann man durch deren
,,Verknüpfung'' weitere Ereignisse bilden. Dies wird durch die
folgenden Mengenoperationen modelliert.
kann man durch deren
,,Verknüpfung'' weitere Ereignisse bilden. Dies wird durch die
folgenden Mengenoperationen modelliert.
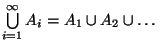 : Menge
aller Elemente, die zu mindestens einer der Mengen
: Menge
aller Elemente, die zu mindestens einer der Mengen 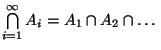 : Menge
aller Elemente, die zu jeder der Mengen
: Menge
aller Elemente, die zu jeder der Mengen 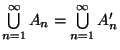
![]() in die Modellierung einzubeziehen, sondern man betrachtet
nur die Familie derjenigen Teilmengen von
in die Modellierung einzubeziehen, sondern man betrachtet
nur die Familie derjenigen Teilmengen von ![]() , deren
Wahrscheinlichkeiten tatsächlich von Interesse sind. Diese
Mengenfamilie soll jedoch abgeschlossen sein bezüglich der
Operationen
, deren
Wahrscheinlichkeiten tatsächlich von Interesse sind. Diese
Mengenfamilie soll jedoch abgeschlossen sein bezüglich der
Operationen
![]() , was durch die folgende
Begriffsbildung erreicht wird.
, was durch die folgende
Begriffsbildung erreicht wird.
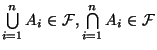
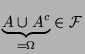 wegen (A2) bzw.
wegen (A2) bzw.
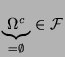 wegen (A1)
wegen (A1)
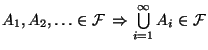 gilt.
gilt.