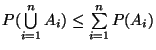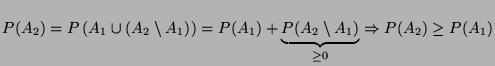Next: Endliche Wahrscheinlichkeitsräume
Up: Ereignisse und Wahrscheinlichkeiten
Previous: Ereignissysteme
Contents
Wahrscheinlichkeitsmaße
Gegeben sei ein Meßraum
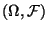 . Betrachten eine
Mengenfunktion, d.h. eine Abbildung
. Betrachten eine
Mengenfunktion, d.h. eine Abbildung
![$ P:\mathcal{F}\rightarrow[0,1]$](img104.png) , die jeder Menge
, die jeder Menge
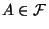 eine
Zahl
eine
Zahl
![$ P(A)\in[0,1]$](img106.png) zuordnet. Dann heißt
zuordnet. Dann heißt 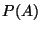 Wahrscheinlichkeit
des Ereignisses
Wahrscheinlichkeit
des Ereignisses
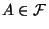 .
.
- Definition 2.9
 Die Mengenfunktion
Die Mengenfunktion
![$ P:\mathcal{F}\rightarrow[0,1]$](img104.png) heißt Wahrscheinlichkeitsmaß auf
heißt Wahrscheinlichkeitsmaß auf
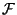 , falls
, falls
- (P1)
-
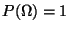 (,,Normiertheit'')
(,,Normiertheit'')
- (P2)
-
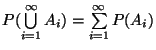 für paarweise disjunkte
für paarweise disjunkte
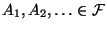 (,,
(,,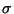 -Additivität'')
-Additivität'')
Falls
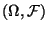 ein Meßraum und
ein Meßraum und 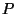 ein
Wahrscheinlichkeitsmaß auf
ein
Wahrscheinlichkeitsmaß auf
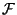 ist, dann heißt das Tripel
ist, dann heißt das Tripel
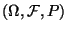 Wahrscheinlichkeitsraum.
Wahrscheinlichkeitsraum.
- Theorem 2.10
 Sei
Sei
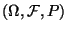 ein
Wahrscheinlichkeitsraum und
ein
Wahrscheinlichkeitsraum und
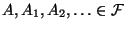 .
Dann gilt
.
Dann gilt
-
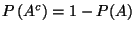
-
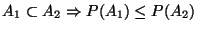
-
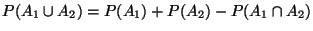
-
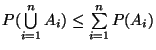
- Beweis
-
-
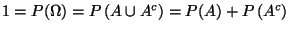
-
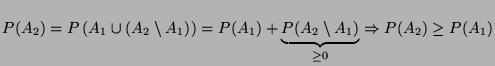
- Wegen
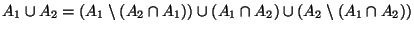 gilt
gilt
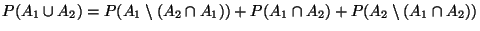 .
.
Weil
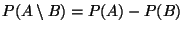 für
für
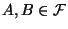 mit
mit
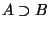 gilt, folgt hieraus die Behauptung.
gilt, folgt hieraus die Behauptung.
- Übungsaufgabe
Roland Maier
2001-08-20
![]() . Betrachten eine
Mengenfunktion, d.h. eine Abbildung
. Betrachten eine
Mengenfunktion, d.h. eine Abbildung
![]() , die jeder Menge
, die jeder Menge
![]() eine
Zahl
eine
Zahl
![]() zuordnet. Dann heißt
zuordnet. Dann heißt ![]() Wahrscheinlichkeit
des Ereignisses
Wahrscheinlichkeit
des Ereignisses
![]() .
.
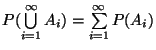 für paarweise disjunkte
für paarweise disjunkte