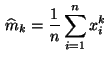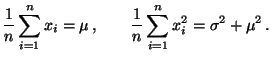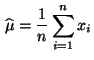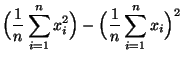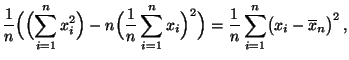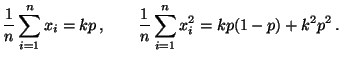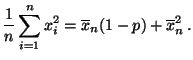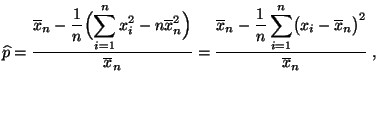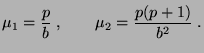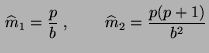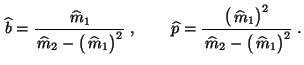Next: Maximum-Likelihood-Schätzer
Up: Methoden zur Gewinnung von
Previous: Methoden zur Gewinnung von
Contents
Momenten-Methode
- Die Momentenmethode ist eines der ältesten Verfahren zur Gewinnung
von Schätzern für die unbekannten Komponenten des Parametervektors
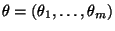 .
.
- Sie wurde von Karl Pearson (1857-1936) gegen Ende des 19.
Jahrhunderts eingeführt und
- beruht auf dem Vergleich von Momenten der Stichprobenvariablen
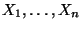 mit den entsprechenden empirischen Momenten der
konkreten Stichprobe
mit den entsprechenden empirischen Momenten der
konkreten Stichprobe
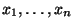 .
.
- Modellannahmen
-
- Lösungsansatz
-
- Für jedes
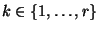 bestimmen wir das
bestimmen wir das 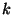 -te empirische Moment
der konkreten Stichprobe
-te empirische Moment
der konkreten Stichprobe
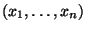 .
.
- Danach bilden wir das Gleichungssystem
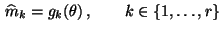 |
(4) |
mit dem unbekannten Vektor
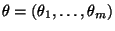 .
.
- Es wird vorausgesetzt, daß dieses Gleichungssystem für jedes
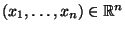 eine eindeutig bestimmte Lösung
eine eindeutig bestimmte Lösung
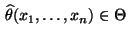 besitzt, die von der
konkreten Stichprobe
besitzt, die von der
konkreten Stichprobe
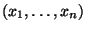 abhängt, und daß
abhängt, und daß
- die Abbildung
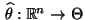 mit
mit
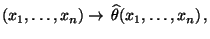 |
(5) |
die den Stichprobenraum
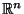 in den Parameterraum
in den Parameterraum
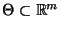 abbildet, Borel-meßbar ist, d.h.,
abbildet, Borel-meßbar ist, d.h.,
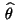 ist eine Stichprobenfunktion.
ist eine Stichprobenfunktion.
- Definition
 Der durch (5) gegebene Zufallsvektor
Der durch (5) gegebene Zufallsvektor
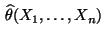 heißt M-Schätzer des
Parametervektors
heißt M-Schätzer des
Parametervektors 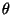 , wobei in (5) die
Zufallsstichprobe
, wobei in (5) die
Zufallsstichprobe
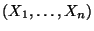 anstelle der konkreten
Stichprobe
anstelle der konkreten
Stichprobe
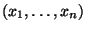 eingesetzt wird.
eingesetzt wird.
- Beachte
-
- Beispiele
-
 Normalverteilte Stichprobenvariablen
Normalverteilte Stichprobenvariablen
 Binomialverteilte Stichprobenvariablen
Binomialverteilte Stichprobenvariablen
- Es gelte nun
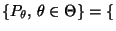 Bin
Bin
![$ (k,p),\,k\in\mathbb{N},\,
p\in[0,1]\}$](img647.png) .
.
- Dabei nehmen wir erneut an, daß beide Komponenten
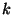 und
und
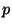 des Parametervektors
des Parametervektors 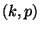 unbekannt sind.
unbekannt sind.
- Dann ist
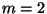 und
und
![% latex2html id marker 26497
$ \Theta=\mathbb{N}\times[0,1]$](img650.png) mit
mit
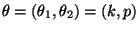 .
.
- Außerdem ist
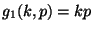
und
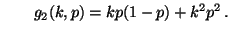
- Das Gleichungssystem (4) hat also die Form
- Durch Einsetzen der ersten Gleichung in die zweite Gleichung
ergibt sich, daß
- Falls nicht sämtliche Stichprobenwerte
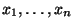 gleich
Null sind, dann ergibt sich hieraus die Lösung
gleich
Null sind, dann ergibt sich hieraus die Lösung
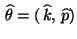 mit
und
wobei sich die letzte Gleichheit erneut aus der Darstellungsformel
(1.15) der Stichprobenvarianz ergibt.
mit
und
wobei sich die letzte Gleichheit erneut aus der Darstellungsformel
(1.15) der Stichprobenvarianz ergibt.
- Bei binomialverteilten Stichprobenvariablen
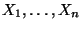 ergeben sich also die M-Schätzer
ergeben sich also die M-Schätzer
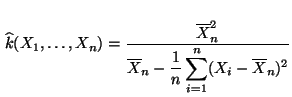 |
(10) |
und
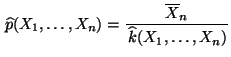 |
(11) |
für die unbekannten Modellparameter 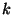 bzw.
bzw. 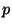 , falls
, falls
 .
.
 Gammaverteilte Stichprobenvariablen
Gammaverteilte Stichprobenvariablen
- Es gelte
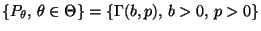 .
.
- Dann ist
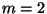 und
und
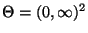 mit
mit
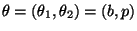 .
.
- Aus Theorem 1.5 folgt, daß
- Hieraus ergibt sich das Geichungssystem
mit der Lösung
- Beachte
-
- Es gibt Beispiele parametrischer Verteilungsfamilien, so daß das
Gleichungssystem (4) für
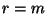 nicht eindeutig lösbar
ist, für
nicht eindeutig lösbar
ist, für 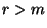 jedoch eine eindeutig bestimmte Lösung besitzt.
jedoch eine eindeutig bestimmte Lösung besitzt.
- D.h., bei der Anwendung der Momentenmethode kann die Anzahl der zu
betrachtenden Momente
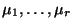 größer als die Anzahl
der (unbekannten) Parameterkomponenten
größer als die Anzahl
der (unbekannten) Parameterkomponenten
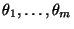 sein, vgl. die Übungsaufgabe 5.2.b.
sein, vgl. die Übungsaufgabe 5.2.b.




Next: Maximum-Likelihood-Schätzer
Up: Methoden zur Gewinnung von
Previous: Methoden zur Gewinnung von
Contents
Roland Maier
2003-03-06