



Next: Asymptotische Eigenschaften von Punktschätzern
Up: Güteeigenschaften von Punktschätzern
Previous: Bedingte Erwartung; Ungleichung von
Contents
Maßtheoretische Definition der bedingten Erwartung
- In Abschnitt 2.3.6 wurde der Begriff der bedingten
Erwartung
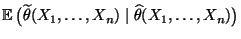 eingeführt, wobei
zunächst die Grenzwerte
eingeführt, wobei
zunächst die Grenzwerte
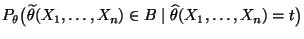 in (48)
betrachtet wurden.
in (48)
betrachtet wurden.
- Diese Vorgehensweise besitzt den Vorteil, daß intuitiv klar wird,
inwiefern
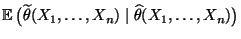 als Funktion von
als Funktion von
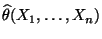 aufgefaßt werden kann.
aufgefaßt werden kann.
- Allerdings wurde dabei nicht näher untersucht,
- ob bzw. unter welchen Bedingungen die Grenzwerte
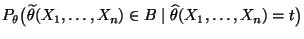 in (48)
existieren,
in (48)
existieren,
- ob sie (bei gegebenem
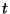 ) eine
) eine 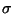 -additive Mengenfunktion
bezüglich
-additive Mengenfunktion
bezüglich 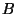 , d.h. ein Wahrscheinlichkeitsmaß über
, d.h. ein Wahrscheinlichkeitsmaß über
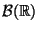 bilden und
bilden und
- ob die Abbildung
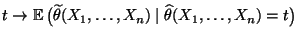 Borel-meßbar ist.
Borel-meßbar ist.
Der folgende (maßtheoretische) Zugang zur bedingten Erwartung
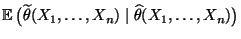 ist zwar weniger
intuitiv, besitzt jedoch den Vorteil, daß er mit den allgemeinen
Rechenregeln der Maß- und Integrationstheorie begründet werden
kann.
ist zwar weniger
intuitiv, besitzt jedoch den Vorteil, daß er mit den allgemeinen
Rechenregeln der Maß- und Integrationstheorie begründet werden
kann.
Aus der Definitionsgleichung (51) und aus den
allgemeinen Rechenregeln für das Lebesgue-Integral ergeben sich
die folgenden Eigenschaften der bedingten Erwartung, die wir hier
lediglich (ohne Beweis) erwähnen.
Theorem 2.8
Seien
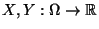
beliebige Zufallsvariablen über
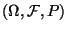
mit
und sei
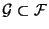
eine beliebige Teil-
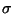
-Algebra
von
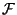
. Dann gilt
- 1.
-
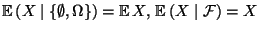 ,
,
- 2.
-
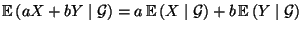 für
beliebige
für
beliebige
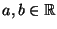 ,
,
- 3.
-
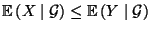 , falls
, falls 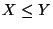 ,
,
- 4.
-
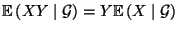 , falls
, falls 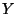 eine
eine
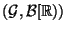 -meßbare Zufallsvariable ist,
-meßbare Zufallsvariable ist,
- 5.
-
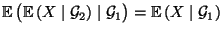 ,
falls
,
falls
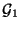 und
und
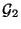 Teil-
Teil-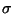 -Algebren von
-Algebren von
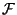 sind mit
sind mit
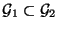 ,
,
- 6.
-
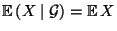 , falls die
, falls die 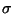 -Algebren
-Algebren
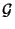 und
und
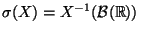 unabhängig sind, d.h., falls
unabhängig sind, d.h., falls
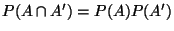 für beliebige
für beliebige
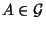 und
und
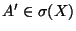 .
.
- Beachte
-
- Aus den Teilaussagen 1 und 5 ergibt sich, daß
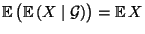 , wenn
, wenn
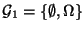 und
und
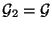 gesetzt wird.
gesetzt wird.
- Aus Teilaussage 2 ergibt sich, daß
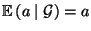 für
beliebige
für
beliebige
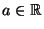 und
und
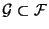 .
.
- Hieraus und aus Teilaussage 4 folgt, daß
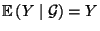 für
jede
für
jede
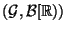 -meßbare Zufallsvariable
-meßbare Zufallsvariable 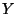 (wenn
(wenn 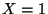 gesetzt wird).
gesetzt wird).
- Beispiel
-
- Seien
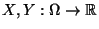 beliebige Zufallsvariablen über
beliebige Zufallsvariablen über
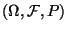 mit
mit
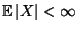 , und sei
, und sei
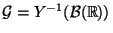 die Teil-
die Teil-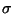 -Algebra von
-Algebra von
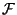 ,
die durch
,
die durch 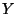 erzeugt wird.
erzeugt wird.
- Dann heißt
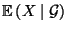 die bedingte Erwartung von
die bedingte Erwartung von 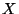 bezüglich
bezüglich 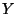 , wobei auch die Schreibweise
, wobei auch die Schreibweise
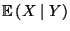 benutzt
wird.
benutzt
wird.
- Insbesondere stimmt die bedingte Erwartung
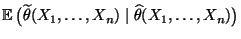 von
von
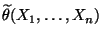 bezüglich
bezüglich
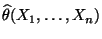 mit dem in
Abschnitt 2.3.6 eingeführten Begriff überein, falls
die Grenzwerte in (48) existieren und
Wahrscheinlichkeitsmaße bilden, deren Erwartungswerte eine in
mit dem in
Abschnitt 2.3.6 eingeführten Begriff überein, falls
die Grenzwerte in (48) existieren und
Wahrscheinlichkeitsmaße bilden, deren Erwartungswerte eine in 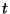 Borel-meßbare Funktion ergeben.
Borel-meßbare Funktion ergeben.




Next: Asymptotische Eigenschaften von Punktschätzern
Up: Güteeigenschaften von Punktschätzern
Previous: Bedingte Erwartung; Ungleichung von
Contents
Roland Maier
2003-03-06
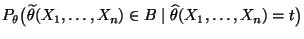 in (48)
existieren,
in (48)
existieren,
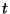 ) eine
) eine 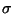 -additive Mengenfunktion
bezüglich
-additive Mengenfunktion
bezüglich 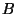 , d.h. ein Wahrscheinlichkeitsmaß über
, d.h. ein Wahrscheinlichkeitsmaß über
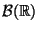 bilden und
bilden und
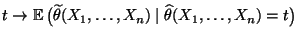 Borel-meßbar ist.
Borel-meßbar ist.
![]() ist zwar weniger
intuitiv, besitzt jedoch den Vorteil, daß er mit den allgemeinen
Rechenregeln der Maß- und Integrationstheorie begründet werden
kann.
ist zwar weniger
intuitiv, besitzt jedoch den Vorteil, daß er mit den allgemeinen
Rechenregeln der Maß- und Integrationstheorie begründet werden
kann.