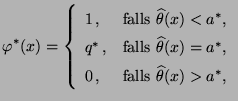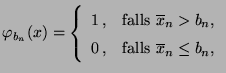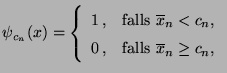Next: Weitere Testprobleme
Up: Gleichmäßig beste Tests
Previous: Suffizienz und monotoner Likelihood-Quotient
Contents
Gleichmäßig beste Tests bei
zusammengesetzten Hypothesen
Bisher haben wir in den Abschnitten 4.5.2 -
4.5.5 stets vorausgesetzt, daß sowohl die
Null-Hypothese 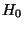 als auch die Alternativ-Hypothese
als auch die Alternativ-Hypothese 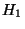 einfache Hypothesen sind.
Nun wollen wir auch zusammengesetzte Hypothesen zulassen, wobei
wir annehmen, daß
einfache Hypothesen sind.
Nun wollen wir auch zusammengesetzte Hypothesen zulassen, wobei
wir annehmen, daß
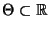 eine offene Teilmenge von
eine offene Teilmenge von
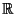 ist.
ist.
- Beweis
-
- Um die Teilaussage
 zu zeigen, wählen wir ein beliebiges
zu zeigen, wählen wir ein beliebiges
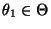 mit
mit
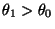 .
.
- Aus Korollar 4.1 folgt dann, daß
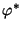 bester
Test ist für die einfachen Hypothesen
bester
Test ist für die einfachen Hypothesen
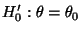
versus
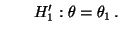
- Weil
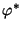 nicht von der Wahl des Parameterwertes
nicht von der Wahl des Parameterwertes
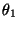 abhängt, ist somit die Teilaussage
abhängt, ist somit die Teilaussage 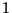 für das
Testproblem
für das
Testproblem
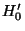 versus
versus 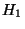 bewiesen.
bewiesen.
- Der Beweis von Teilaussage
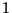 ist beendet, wenn noch gezeigt
wird, daß
ist beendet, wenn noch gezeigt
wird, daß
- Dies ergibt sich jedoch aus dem Beweis von Teilaussage
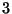 , d.h.
aus der dort nachzuweisenden Monotonie der Gütefunktion von
, d.h.
aus der dort nachzuweisenden Monotonie der Gütefunktion von
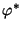 .
.
- Der Beweis von Teilaussage
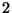 , d.h., die Bestimmung von
Konstanten
, d.h., die Bestimmung von
Konstanten
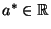 und
und
![$ q^*\in[0,1]$](img2438.png) , so daß
für beliebige, jedoch vorgegebene
, so daß
für beliebige, jedoch vorgegebene
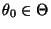 und
und
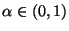 verläuft genauso der Beweis der Existenzaussage
des Fundamentallemmas von Neyman-Pearson (vgl.
Theorem 4.2).
verläuft genauso der Beweis der Existenzaussage
des Fundamentallemmas von Neyman-Pearson (vgl.
Theorem 4.2).
- Es bleibt nun noch die Gültigkeit von Teilaussage
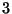 zu zeigen,
d.h.,
zu zeigen,
d.h.,
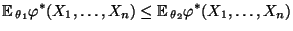 |
(63) |
für beliebige Parameterwerte
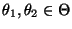 mit
mit
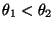 .
.
- Hierfür betrachten wir die einfachen Hypothesen
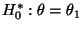
versus
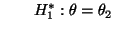
und vergleichen wir den in
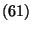 gegebenen Test
gegebenen Test
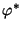 mit dem (konstanten) Test
mit dem (konstanten) Test
![$ \varphi:\mathbb{R}^n\to[0,1]$](img2190.png) ,
wobei
,
wobei
- Gemäß Korollar 4.1 ist
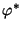 bester Test zum
Niveau
bester Test zum
Niveau
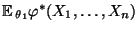 . Die Macht
. Die Macht
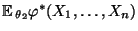 von
von 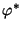 bei
bei
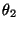 ist deshalb nicht kleiner als die Macht
von
ist deshalb nicht kleiner als die Macht
von 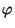 bei
bei 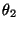 .
.

- Beachte
-
-
- Auf analoge Weise wie im Beweis von Theorem 4.6 läßt
sich zeigen, daß zum Prüfen der Hypothesen
ein gleichmäßig bester Test
![$ \varphi^*:\mathbb{R}^n\to[0,1]$](img2439.png) zum Niveau
zum Niveau
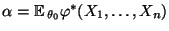 durch den Ansatz
gegeben ist, wobei
durch den Ansatz
gegeben ist, wobei
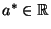 ,
,
![$ q^*\in[0,1]$](img2438.png) .
.
- Beispiel
 Normalverteilte Stichprobenvariablen
Normalverteilte Stichprobenvariablen




Next: Weitere Testprobleme
Up: Gleichmäßig beste Tests
Previous: Suffizienz und monotoner Likelihood-Quotient
Contents
Roland Maier
2003-03-06