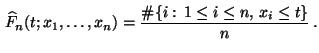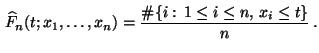Next: -Anpassungstest
Up: Weitere Testprobleme
Previous: Weitere Testprobleme
Contents
Kolmogorow-Test
- Zur Überprüfung der Hypothesen
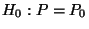 versus versus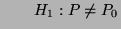 |
(64) |
werden in der Literatur verschiedene asymptotische Tests
vorgeschlagen.
- Ein solches Verfahren ist beispielsweise der
Kolmogorow-Test, bei dem vorausgesetzt wird, daß die zu
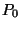 gehörende hypothetische Verteilungsfunktion
gehörende hypothetische Verteilungsfunktion
![$ F_0:\mathbb{R}\to[0,1]$](img2250.png) stetig ist.
stetig ist.
- Der Kolmogorow-Test beruht auf der Untersuchung der in
Abschnitt 1.5 eingeführten empirischen
Verteilungsfunktion
![$ \,\widehat F_n:\mathbb{R}\times\mathbb{R}^n\to[0,1]$](img2531.png) ,
wobei
,
wobei
- Dabei wird die Testgröße
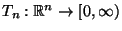 betrachtet mit
betrachtet mit
- In Theorem 1.20 hatten wir erwähnt, daß unter
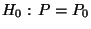 gilt, wobei
gilt, wobei
![$\displaystyle K(x)=\left\{\begin{array}{ll} 1-2\sum\limits_{k=1}^\infty
(-1)^{...
...box{falls $x>0$,}\\ [3\jot]
0\,, & \mbox{falls $x\le 0$.}
\end{array}\right.$](img575.png) |
(65) |
- Bei hinreichend großem Stichprobenumfang (als ,,Faustregel'' gilt
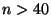 , vgl. die Bemerkung am Ende von
Abschnitt 1.5.3) wird die Hypothese
, vgl. die Bemerkung am Ende von
Abschnitt 1.5.3) wird die Hypothese 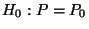 deshalb abgelehnt, falls
deshalb abgelehnt, falls
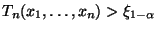 ,
wobei
,
wobei
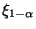 das
das
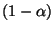 -Quantil der in
(65) gegebenen Kolmogorow-Verteilung
bezeichnet, d.h.,
-Quantil der in
(65) gegebenen Kolmogorow-Verteilung
bezeichnet, d.h.,
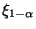 ist Lösung der Gleichung
ist Lösung der Gleichung
- Falls
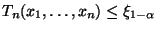 , dann wird die
Hypothese
, dann wird die
Hypothese 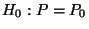 nicht abgelehnt.
nicht abgelehnt.




Next: -Anpassungstest
Up: Weitere Testprobleme
Previous: Weitere Testprobleme
Contents
Roland Maier
2003-03-06