Next: Anwendungsbeispiele: Monte-Carlo-Simulation
Up: Weitere Testprobleme
Previous: Kolmogorow-Test
Contents
 -Anpassungstest
-Anpassungstest
Wir modifizieren nun die ursprüngliche Fragestellung
(64) auf die folgende Weise:
Wir zeigen zunächst den folgenden Hilfssatz.
- Beweis
-
- Beachte
-
Anstelle das ursprüngliche Testproblem (64) zu
untersuchen, prüfen wir nun
Das folgende Theorem ist die Grundlage des sogenannten
 -Anpassungstests, der von Karl Pearson (1857-1936)
eingeführt worden ist.
-Anpassungstests, der von Karl Pearson (1857-1936)
eingeführt worden ist.
Theorem 4.7
Für jedes
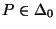
gilt
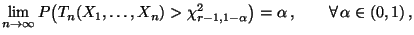 |
(70) |
wobei
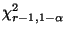
das
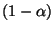
-Quantil der
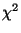
-Verteilung mit
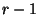
Freiheitsgraden bezeichnet.
Der Beweis von Theorem 4.7 geht über den
Rahmen dieser einführenden Vorlesung hinaus. Die Beweisidee beruht
auf der Anwendung des
- zentralen Grenzwertsatzes für Summen von unabhängigen und
identisch verteilten Zufallsvektoren (der eine mehrdimensionale
Version von Theorem WR-5.16 ist) und
- des Continuous Mapping Theorems für Zufallsvektoren (eine
mehrdimensionale Version von Theorem WR-5.12).
Dabei wird die Tatsache genutzt, daß
vgl. beispielsweise Abschnitt 11.2 in H.-O. Georgii (2002)
Stochastik: Einführung in die Wahrscheinlichkeitstheorie und
Statistik, de Gruyter, Berlin oder Abschnitt II.3 in H. Pruscha
(1996) Angewandte Methoden der Mathematischen Statistik,
Teubner, Stuttgart.
- Beachte
-
- Bei der praktischen Durchführung des
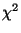 -
Anpassungstests zur Prüfung der Hypothese
-
Anpassungstests zur Prüfung der Hypothese 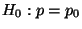 (gegen die
Alternative
(gegen die
Alternative
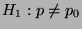 ) ist zunächst der Wert der in
(69) definierten Testgröße
) ist zunächst der Wert der in
(69) definierten Testgröße
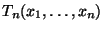 zu
berechnen.
zu
berechnen.
- Bei hinreichend großem Stichprobenumfang
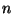 wird die Hypothese
wird die Hypothese
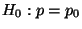 abgelehnt, falls
abgelehnt, falls
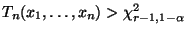 , wobei
, wobei
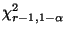 das
das
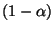 -Quantil der
-Quantil der
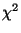 -Verteilung mit
-Verteilung mit 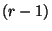 -Freiheitsgraden bezeichnet.
-Freiheitsgraden bezeichnet.
- Falls
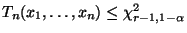 , dann wird
die Hypothese
, dann wird
die Hypothese 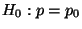 nicht abgelehnt.
nicht abgelehnt.
- Eine ,,Faustregel'' dafür, daß
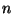 hinreichend groß ist, ist die
Gültigkeit der Ungleichung
hinreichend groß ist, ist die
Gültigkeit der Ungleichung
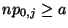 für jedes
für jedes
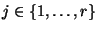 und für eine Konstante
und für eine Konstante 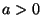 .
.
- Über die erforderliche Größe von
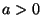 gibt es unterschiedliche
Auffassungen in der Literatur, die von
gibt es unterschiedliche
Auffassungen in der Literatur, die von 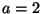 bis
bis 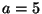 reichen.
Manche Autoren fordern sogar, daß
reichen.
Manche Autoren fordern sogar, daß 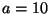 .
.
- Andere Autoren meinen, daß bei einer großen Zahl von Klassen (etwa
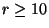 ) auch schon für
) auch schon für 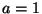 die Approximation hinreichend gut
ist.
die Approximation hinreichend gut
ist.




Next: Anwendungsbeispiele: Monte-Carlo-Simulation
Up: Weitere Testprobleme
Previous: Kolmogorow-Test
Contents
Roland Maier
2003-03-06
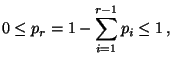
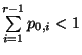 .
.
![]() -Anpassungstests, der von Karl Pearson (1857-1936)
eingeführt worden ist.
-Anpassungstests, der von Karl Pearson (1857-1936)
eingeführt worden ist.