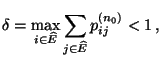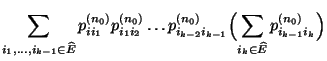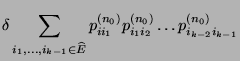Nächste Seite: Abschätzung der Konvergenzgeschwindigkeit; Reversibilität
Aufwärts: Ergodizität und Stationarität
Vorherige Seite: Stationäre Anfangsverteilungen
Inhalt
Direkte und iterative Berechnungsmethoden
Wir zeigen nun, wie die stationäre Anfangsverteilung
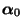
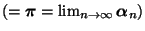 der Markov-Kette
der Markov-Kette
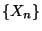 mit Methoden der linearen Algebra berechnet werden kann,
falls die Übergangsmatrix
mit Methoden der linearen Algebra berechnet werden kann,
falls die Übergangsmatrix
 nicht speziell strukturiert
(jedoch quasi-positiv) ist und falls die Anzahl
nicht speziell strukturiert
(jedoch quasi-positiv) ist und falls die Anzahl 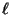 der
Zustände nicht zu groß ist.
der
Zustände nicht zu groß ist.
- Beweis
-
- Um zu beweisen, dass die Matrix
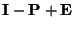 invertierbar
ist, zeigen wir, dass die einzige Lösung der Gleichung
invertierbar
ist, zeigen wir, dass die einzige Lösung der Gleichung
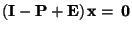 |
(74) |
durch
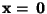 gegeben ist.
gegeben ist.
- Weil
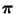 der Gleichung
der Gleichung
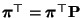 genügt,
gilt auch
genügt,
gilt auch
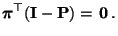 |
(75) |
- Somit folgt aus (74), dass
d.h.
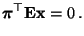 |
(76) |
- Andererseits gilt offenbar
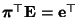 und somit
wegen (76) auch
und somit
wegen (76) auch
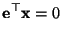 bzw. bzw.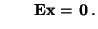 |
(77) |
- Hieraus und aus (74) folgt, dass
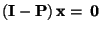 bzw.
bzw.
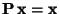 .
.
- Damit gilt auch
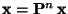 für jedes
für jedes 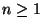 .
.
- Aus Theorem 2.4 ergibt sich nun, dass
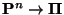 ,
,
- Die Matrix
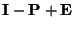 ist also invertierbar.
ist also invertierbar.
- Wegen (75) ergibt sich schließlich, dass
bzw.

- Beachte
-
- Beweis
-
- Beweis
-
- Beachte
-




Nächste Seite: Abschätzung der Konvergenzgeschwindigkeit; Reversibilität
Aufwärts: Ergodizität und Stationarität
Vorherige Seite: Stationäre Anfangsverteilungen
Inhalt
Ursa Pantle
2003-09-29
![]()
![]() der Markov-Kette
der Markov-Kette
![]() mit Methoden der linearen Algebra berechnet werden kann,
falls die Übergangsmatrix
mit Methoden der linearen Algebra berechnet werden kann,
falls die Übergangsmatrix
![]() nicht speziell strukturiert
(jedoch quasi-positiv) ist und falls die Anzahl
nicht speziell strukturiert
(jedoch quasi-positiv) ist und falls die Anzahl ![]() der
Zustände nicht zu groß ist.
der
Zustände nicht zu groß ist.