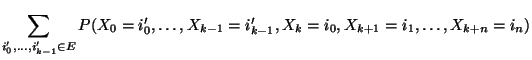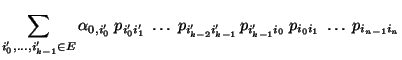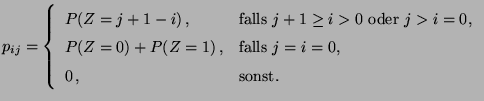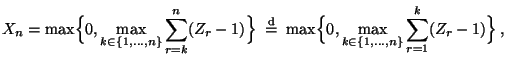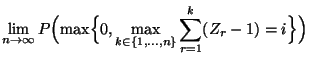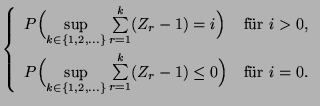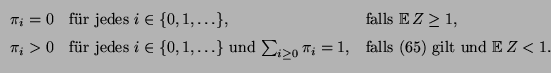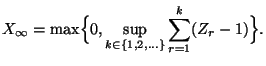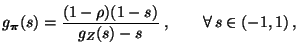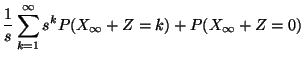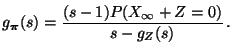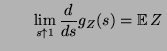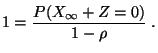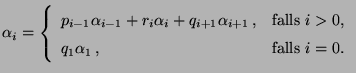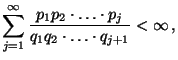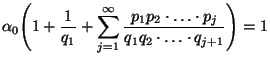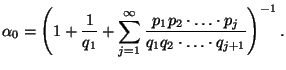Nächste Seite: Direkte und iterative Berechnungsmethoden
Aufwärts: Ergodizität und Stationarität
Vorherige Seite: Irreduzibilität und Aperiodizität
Inhalt
Stationäre Anfangsverteilungen
- Zur Erinnerung
- Wenn nicht vorausgesetzt wird, dass die Markov-Kette
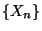 irreduzibel ist, dann kann (59) mehr als eine
(Wahrscheinlichkeits-) Lösung besitzen.
irreduzibel ist, dann kann (59) mehr als eine
(Wahrscheinlichkeits-) Lösung besitzen.
- Umgekehrt kann man zeigen, dass,
- die Matrix-Gleichung (59) genau eine
(Wahrscheinlichkeits-) Lösung
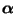 besitzt, falls
besitzt, falls
 irreduzibel ist,
irreduzibel ist,
- wobei diese Lösung
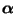 von (59) jedoch nicht notwendig die Grenzverteilung
von (59) jedoch nicht notwendig die Grenzverteilung
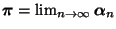 sein muss, die nämlich dann
nicht existiert, falls
sein muss, die nämlich dann
nicht existiert, falls
 nicht aperiodisch ist.
nicht aperiodisch ist.
Einen Beweis von Theorem 2.10 kann man
beispielsweise in Kapitel 7 des Buches E. Behrends (2000) Introduction to Markov Chains, Vieweg, Braunschweig finden.
- Beachte
-
- Außer der Invarianzeigenschaft
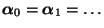 besitzt die Markov-Kette
besitzt die Markov-Kette 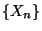 mit der stationären
Anfangsverteilung
mit der stationären
Anfangsverteilung
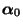 noch eine wesentlich stärkere
Invarianzeigenschaft (und zwar für sämtliche endlich-dimensionalen
Verteilungen).
noch eine wesentlich stärkere
Invarianzeigenschaft (und zwar für sämtliche endlich-dimensionalen
Verteilungen).
- In diesem Zusammenhang betrachten wir den folgenden Begriff der
(streng) stationären Folge von Zufallsvariablen.
- Definition
-
Theorem 2.11
- Sei
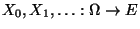 eine Markov-Kette mit dem
Zustandsraum
eine Markov-Kette mit dem
Zustandsraum
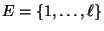 .
.
- Die Markov-Kette
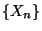 ist genau dann eine stationäre Folge
von Zufallsvariablen, wenn sie eine stationäre Anfangsverteilung
besitzt.
ist genau dann eine stationäre Folge
von Zufallsvariablen, wenn sie eine stationäre Anfangsverteilung
besitzt.
- Beweis
-
- Die Notwendigkeit der Bedingung ergibt sich unmittelbar
- aus Theorem 2.3 sowie aus den
Definitionen der Begriffe ,,stationäre Anfangsverteilung'' bzw.
,,stationäre Folge von Zufallsvariablen'',
- denn die Gültigkeit von (62) impliziert
insbesondere, dass
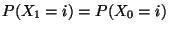 für jedes
für jedes 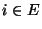
- und aus Theorem 2.3 ergibt sich somit, dass
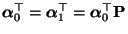 , d.h.
, d.h.
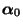 ist eine stationäre Anfangsverteilung.
ist eine stationäre Anfangsverteilung.
- Sei nun umgekehrt
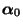 eine stationäre Anfangsverteilung
der Markov-Kette
eine stationäre Anfangsverteilung
der Markov-Kette 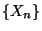 .
.
- Beachte
-
- Für einige Beispiele von Markov-Ketten mit speziell strukturierten
Übergangsmatrizen hatten wir bereits in den
Abschnitten 2.2.2 und 2.2.3 die
zugehörigen stationären Anfangsverteilungen bestimmt.
- Wir diskutieren nun noch zwei weitere Beispiele dieses Typs.
- Der Zustandsraum ist dabei jeweils unendlich, so dass außer
der Quasi-Positivität (bzw. der Irreduzibilität und Aperiodizität
der Übergangsmatrix) noch eine weitere Bedingung erforderlich ist,
um die Ergodizität der betrachteten Markov-Ketten zu garantieren.
- Es ist dies eine sogenannte Kontraktionsbedingung, die
verhindert, dass die ,,Wahrscheinlichkeitsmasse'' ins Unendliche
abdriftet.
- Beispiele
-
- Warteschlangen
vgl. T. Rolski, H. Schmidli, V. Schmidt, J. Teugels (2002)
Stochastic Processes for Insurance and Finance.
J. Wiley & Sons, Chichester, S. 147 ff.
- Wir betrachten das bereits in Abschnitt 2.1.2
diskutierte Beispiel
- der rekursiv definierten Markov-Kette
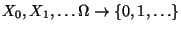 mit
mit 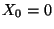 und
und
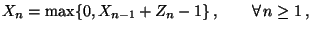 |
(63) |
- wobei die Zufallsvariablen
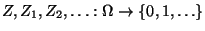 unabhängig und
identisch verteilt sind und die Übergangsmatrix
unabhängig und
identisch verteilt sind und die Übergangsmatrix
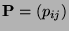 gegeben ist durch
gegeben ist durch
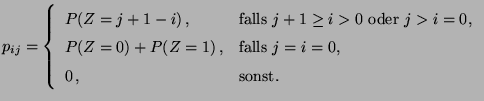 |
(64) |
- Man kann zeigen, dass
- die in (63) rekursiv definierte Markov-Kette
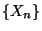 bzw. die zugehörige (in (64) gegebene)
Übergangsmatrix irreduzibel und aperiodisch ist, falls
bzw. die zugehörige (in (64) gegebene)
Übergangsmatrix irreduzibel und aperiodisch ist, falls
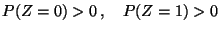 und und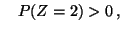 |
(65) |
- die Lösung der Rekursionsgleichung (63) sich
für jedes
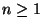 darstellen lässt in der Form
darstellen lässt in der Form
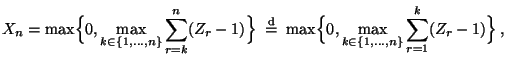 |
(66) |
- die (Grenz-) Wahrscheinlichkeiten
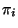 für jedes
für jedes
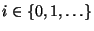 existieren, wobei
existieren, wobei
Dabei gilt
- Für Markov-Ketten mit (abzählbar) unendlichem Zustandsraum
- folgt also die Ergodizität im allgemeinen nicht aus der
Irreduzibilität und Aperiodizität,
- sondern es muss noch zusätzlich eine gewisse Kontraktionsbedingung erfüllt sein,
- wobei dies im Fall des hier betrachteten Beispiels die Bedingung
ist, dass die Markov-Kette
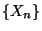 eine negative Drift
besitzt, d.h., dass
eine negative Drift
besitzt, d.h., dass
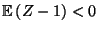 gilt.
gilt.
- Falls die Bedingungen (65) erfüllt sind und
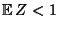 gilt,
gilt,
- Beweis von (68)
- Aus (67) ergibt sich, dass
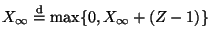 .
.
- Mit der Schreibweise
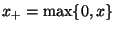 gilt somit
gilt somit
d.h.,
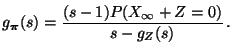 |
(69) |
- Weil
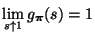
und
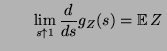
ergibt sich aus der Regel von L'Hospital, dass
- Somit ergibt sich (68) aus (69).
- Geburts- und Todesprozesse mit einer reflektierenden
Schranke
- Wir modifizieren das in Abschnitt 2.2.3 diskutierte
Beispiel des Geburts- und Todesprozesses dahingehend, dass wir nun
den (unendlichen) Zustandsraum
 und die
Übergangsmatrix
und die
Übergangsmatrix
 |
(70) |
betrachten, wobei 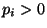 ,
, 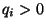 und
und
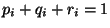 für jedes
für jedes
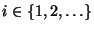 vorausgesetzt wird.
vorausgesetzt wird.
- Das lineare Gleichungssystem
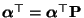 hat dann die Form
hat dann die Form
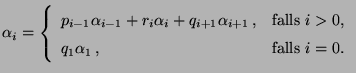 |
(71) |
- Ähnlich wie bei Geburts- und Todesprozessen mit zwei
reflektierenden Schranken kann man zeigen, dass
- das Gleichungssystem (71) eine (eindeutig
bestimmte) Wahrscheinlichkeitslösung
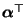 besitzt,
falls
besitzt,
falls
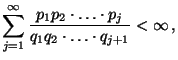 |
(72) |
- die Lösung
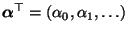 von
(71) in diesem Fall gegeben ist durch
von
(71) in diesem Fall gegeben ist durch
- wobei
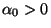 durch die Normierungsbedingung
durch die Normierungsbedingung
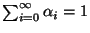 gegeben ist, d.h.
bzw.
gegeben ist, d.h.
bzw.
- Weil wir voraussetzen, dass
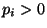 und
und 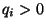 für jedes
für jedes
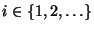 gilt, sind Geburts- und Todesprozesse mit
einer reflektierenden Schranke offenbar irreduzibel.
gilt, sind Geburts- und Todesprozesse mit
einer reflektierenden Schranke offenbar irreduzibel.
- Wenn zusätzlich
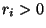 für ein
für ein
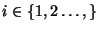 gilt, dann
sind Geburts- und Todesprozesse mit einer reflektierenden
Schranke auch aperiodisch (sowie ergodisch, falls die
Kontraktionsbedingung (72) erfüllt ist).
gilt, dann
sind Geburts- und Todesprozesse mit einer reflektierenden
Schranke auch aperiodisch (sowie ergodisch, falls die
Kontraktionsbedingung (72) erfüllt ist).




Nächste Seite: Direkte und iterative Berechnungsmethoden
Aufwärts: Ergodizität und Stationarität
Vorherige Seite: Irreduzibilität und Aperiodizität
Inhalt
Ursa Pantle
2003-09-29
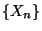 eine irreduzible und aperiodische Markov-Kette mit
dem (endlichen) Zustandsraum
eine irreduzible und aperiodische Markov-Kette mit
dem (endlichen) Zustandsraum
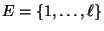 und der
(quasi-positiven) Übergangsmatrix
und der
(quasi-positiven) Übergangsmatrix
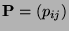 ist,
ist,
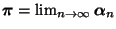 die eindeutig bestimmte Lösung der folgenden Matrix-Gleichung
(vgl. Theorem 2.5):
die eindeutig bestimmte Lösung der folgenden Matrix-Gleichung
(vgl. Theorem 2.5):