



Nächste Seite: Dirichlet-Formen und Rayleigh-Theorem
Aufwärts: Abschätzung der Konvergenzgeschwindigkeit; Reversibilität
Vorherige Seite: Multiplikativ reversible Version der
Inhalt
Alternative Abschätzung der Konvergenzgeschwindigkeit;
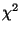 -Kontrast
-Kontrast
Mit Hilfe der multiplikativ reversiblen Version
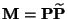 der (ergodischen, jedoch nicht
notwendig reversiblen) Übergangsmatrix
der (ergodischen, jedoch nicht
notwendig reversiblen) Übergangsmatrix
 leiten wir nun eine
alternative Abschätzung für die Geschwindigkeit der Konvergenz
leiten wir nun eine
alternative Abschätzung für die Geschwindigkeit der Konvergenz
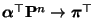 her, wenn
her, wenn
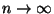 ; vgl.
Theorem 2.16.
; vgl.
Theorem 2.16.
Dabei erweisen sich die folgenden (abkürzenden) Bezeichnungen und
Hilfssätze im Beweis von Theorem 2.16 als nützlich.
- Beweis
-
- Mit der Schreibweise
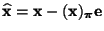 gilt, dass
gilt, dass
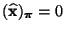 und
wobei sich die vorletzte Gleichheit aus der Definitionsgleichung
(99) der Matrix
und
wobei sich die vorletzte Gleichheit aus der Definitionsgleichung
(99) der Matrix
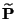 ergibt.
ergibt.
- Hieraus folgt, dass
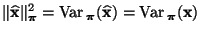 und und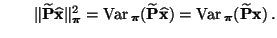 |
(107) |
- Andererseits gilt
und somit
weil
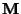 eine stochastische Matrix ist mit
eine stochastische Matrix ist mit
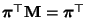 und weil deshalb
und weil deshalb
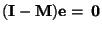 bzw.
bzw.
- Hieraus und aus (107) ergibt sich die
Behauptung.

Wir führen nun noch die folgenden Begriffe ein.
Der Abstand
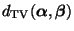 zwischen
zwischen
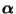 und
und
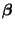 kann wie folgt durch den
kann wie folgt durch den 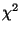 -Kontrast
-Kontrast
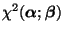 von
von
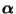 bezüglich
bezüglich
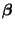 abgeschätzt werden.
abgeschätzt werden.
- Beweis
-
- Aus der Ungleichung von Cauchy-Schwarz ergibt sich unter
Berücksichtigung von
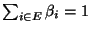 , dass
, dass
- Hieraus folgt die Behauptung.

Die Geschwindigkeit der Konvergenz
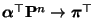 , wenn
, wenn
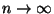 , lässt
sich nun wie folgt
, lässt
sich nun wie folgt
- mit Hilfe des zweitgrößten Eigenwertes
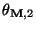 der
multiplikativ reversiblen Version
der
multiplikativ reversiblen Version
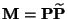 der
(ergodischen) Übergangsmatrix
der
(ergodischen) Übergangsmatrix
 sowie
sowie
- des
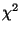 -Kontrastes
-Kontrastes
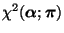 der
Anfangsverteilung
der
Anfangsverteilung
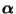 bezüglich der stationären
Grenzverteilung
bezüglich der stationären
Grenzverteilung
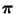 abschätzen.
abschätzen.
Theorem 2.16

Für jede beliebige Anfangsverteilung
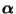
und für jedes
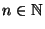
gilt
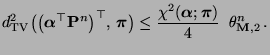 |
(112) |
- Beweis
-
- Sei
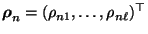 mit
mit
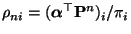 .
.
- Dann gilt für jedes
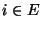 und somit
und somit
- Außerdem ergibt sich aus der Definitionsgleichung
(110) des
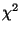 -Kontrastes
-Kontrastes
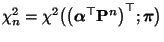 von
von
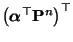 bezüglich
bezüglich
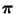 ,
dass
,
dass
d.h.,
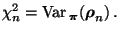 |
(113) |
- Wegen der in Lemma 2.6 hergeleiteten Identität
(106) gilt somit, dass
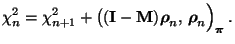 |
(114) |
- Andererseits ergibt sich aus der Spektraldarstellung
(101) von
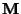 , die in Theorem 2.15
hergeleitet wurde, dass
, die in Theorem 2.15
hergeleitet wurde, dass
weil
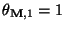 ,
,
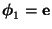 bzw.
bzw.
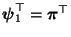 und somit
und somit
- Insgesamt haben wir also gezeigt, dass




Nächste Seite: Dirichlet-Formen und Rayleigh-Theorem
Aufwärts: Abschätzung der Konvergenzgeschwindigkeit; Reversibilität
Vorherige Seite: Multiplikativ reversible Version der
Inhalt
Ursa Pantle
2003-09-29
![]() der (ergodischen, jedoch nicht
notwendig reversiblen) Übergangsmatrix
der (ergodischen, jedoch nicht
notwendig reversiblen) Übergangsmatrix
![]() leiten wir nun eine
alternative Abschätzung für die Geschwindigkeit der Konvergenz
leiten wir nun eine
alternative Abschätzung für die Geschwindigkeit der Konvergenz
![]() her, wenn
her, wenn
![]() ; vgl.
Theorem 2.16.
; vgl.
Theorem 2.16.
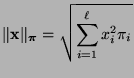
![]() zwischen
zwischen
![]() und
und
![]() kann wie folgt durch den
kann wie folgt durch den ![]() -Kontrast
-Kontrast
![]() von
von
![]() bezüglich
bezüglich
![]() abgeschätzt werden.
abgeschätzt werden.
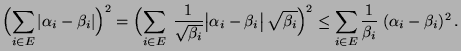
![]() , wenn
, wenn
![]() , lässt
sich nun wie folgt
, lässt
sich nun wie folgt