



Nächste Seite: Beispiel: Hard-Core-Modell
Aufwärts: Monte-Carlo-Simulation
Vorherige Seite: Quotienten von gleichverteilten Zufallsvariablen
Inhalt
Simulationsmethoden mit Markov-Ketten
- Sei
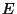 eine beliebige endliche Menge, beispielsweise eine gewisse
Menge von (potentiell möglichen) digitalisierten Binär- bzw.
Graustufenbildern
eine beliebige endliche Menge, beispielsweise eine gewisse
Menge von (potentiell möglichen) digitalisierten Binär- bzw.
Graustufenbildern
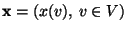 ,
,
- wobei
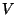 eine endliche Menge von Pixeln ist,
eine endliche Menge von Pixeln ist,
- jedem Pixel
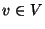 aus dem ,,Beobachtungsfenster''
aus dem ,,Beobachtungsfenster'' 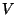 ein
Graustufenwert
ein
Graustufenwert 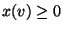 zugeordnet wird,
zugeordnet wird,
- so dass eine ,,Matrix''
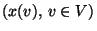 mit bestimmten
Eigenschaften entsteht.
mit bestimmten
Eigenschaften entsteht.
- Sei
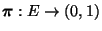 eine beliebige (Wahrscheinlichkeits-)
Funktion mit
eine beliebige (Wahrscheinlichkeits-)
Funktion mit
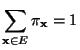
und
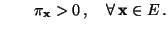
- Wenn die Anzahl
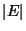 der Elemente der Menge
der Elemente der Menge 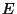 groß ist,
groß ist,
- dann führt die in Abschnitt 3.2 diskutierte
Inversionsmethode bzw. die Akzeptanz- und Verwerfungsmethode
typischerweise nicht zu effizienten Algorithmen,
- um gemäß
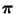 verteilte Pseudozufallselemente
verteilte Pseudozufallselemente
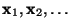 aus
aus 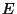 zu erzeugen.
zu erzeugen.
- Beachte
-
- Eine alternative Simulationsmethode beruht
- auf der Konstruktion einer Markov-Kette
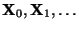 mit dem Zustandsraum
mit dem Zustandsraum 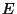
- und mit einer (geeignet gewählten) irreduziblen und aperiodischen
Übergangsmatrix
 ,
,
- so dass
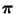 die ergodische (Grenz-) Verteilung der
Markov-Kette ist.
die ergodische (Grenz-) Verteilung der
Markov-Kette ist.
- Für hinreichend großes
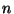
- ist dann
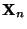 näherungsweise
näherungsweise
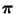 -verteilt und
-verteilt und
- kann somit in vielen Fällen zur effizienten Erzeugung von
(näherungsweise)
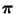 -verteilten Pseudozufallselementen aus
-verteilten Pseudozufallselementen aus
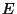 dienen.
dienen.
- Man spricht deshalb in diesem Zusammenhang von Markov-Chain-Monte-Carlo-Simulation (MCMC).
Unterabschnitte




Nächste Seite: Beispiel: Hard-Core-Modell
Aufwärts: Monte-Carlo-Simulation
Vorherige Seite: Quotienten von gleichverteilten Zufallsvariablen
Inhalt
Ursa Pantle
2003-09-29
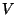 eine endliche Menge von Pixeln ist,
eine endliche Menge von Pixeln ist,
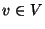 aus dem ,,Beobachtungsfenster''
aus dem ,,Beobachtungsfenster'' 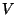 ein
Graustufenwert
ein
Graustufenwert 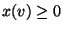 zugeordnet wird,
zugeordnet wird,
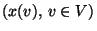 mit bestimmten
Eigenschaften entsteht.
mit bestimmten
Eigenschaften entsteht.
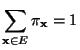 und
und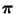 verteilte Pseudozufallselemente
verteilte Pseudozufallselemente
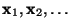 aus
aus 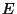 zu erzeugen.
zu erzeugen.