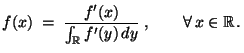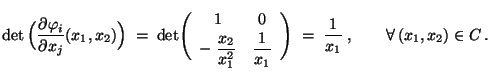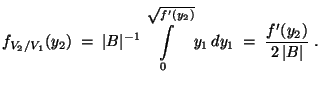Nächste Seite: Simulationsmethoden mit Markov-Ketten
Aufwärts: Transformation gleichverteilter Pseudozufallszahlen
Vorherige Seite: Akzeptanz- und Verwerfungsmethode
Inhalt
Quotienten von gleichverteilten
Zufallsvariablen
In vielen Fällen lassen sich Zufallsvariablen mit absolutstetigen
Verteilungen als Quotienten von gleichverteilten Zufallsvariablen
darstellen.
- In Kombination mit der in Abschnitt 3.2.3 diskutierten
Akzeptanz- und Verwerfungsmethode führt dies zu einem weiteren Typ
von Simulationsalgorithmen.
- Um dies zu präzisieren, benötigen wir den folgenden
Transformationssatz für die Dichte von absolutstetigen
Zufallsvektoren, der bereits in Abschnitt 1.3.2 der Vorlesung
,,Statistik I'' erwähnt wurde.
Aus Theorem 3.8 ergibt sich nun das folgende
Resultat über die Darstellung von Zufallsvariablen mit
absolutstetigen Verteilungen als Quotienten von gleichverteilten
Zufallsvariablen.
Theorem 3.9
- Sei
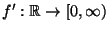 eine (Borel-messbare) beschränkte
Funktion mit
eine (Borel-messbare) beschränkte
Funktion mit
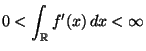 und und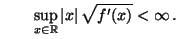 |
(27) |
- Der Zufallsvektor
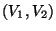 sei gleichverteilt in der
(beschränkten) Borel-Menge
sei gleichverteilt in der
(beschränkten) Borel-Menge
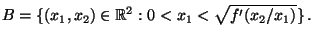 |
(28) |
- Dann ist der Quotient
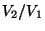 eine absolutstetige
Zufallsvariable mit der Dichte
eine absolutstetige
Zufallsvariable mit der Dichte
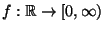 , wobei
, wobei
- Beweis
-
- Beispiel
 (Normalverteilung)
(Normalverteilung)




Nächste Seite: Simulationsmethoden mit Markov-Ketten
Aufwärts: Transformation gleichverteilter Pseudozufallszahlen
Vorherige Seite: Akzeptanz- und Verwerfungsmethode
Inhalt
Ursa Pantle
2003-09-29
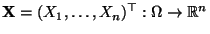 ein
absolutstetiger Zufallsvektor mit der (gemeinsamen) Dichte
ein
absolutstetiger Zufallsvektor mit der (gemeinsamen) Dichte
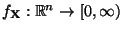 , und sei
, und sei
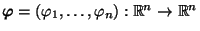 eine
Borel-messbare Abbildung mit stetigen partiellen Ableitungen
eine
Borel-messbare Abbildung mit stetigen partiellen Ableitungen
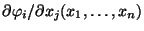 .
.
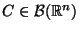 so gewählt, dass
und
so gewählt, dass
und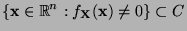 so daß die Einschränkung
so daß die Einschränkung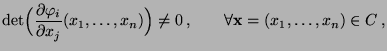
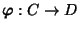 von
von
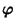 auf
die Menge
auf
die Menge 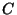 eine eineindeutige Abbildung ist, wobei
eine eineindeutige Abbildung ist, wobei
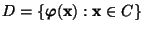 .
.
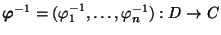 die Umkehrung der Abbildung
die Umkehrung der Abbildung
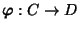 .
.
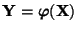 absolutstetig, und für die Dichte
absolutstetig, und für die Dichte
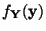 von
von
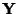 gilt
gilt
![$\displaystyle f_{\mathbf{Y}}({\mathbf{y}})=\left\{\begin{array}{ll} f_{\mathbf{...
...D$,}\\ [3\jot] 0\,, & \mbox{falls ${\mathbf{y}}\not\in D$.} \end{array}\right.$](img1459.png)
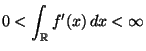 und
und