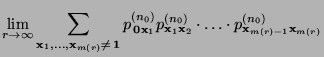- (a)
-
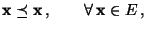
- (b)
- aus
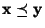 und
und
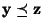 folgt
folgt
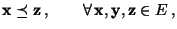
- (c)
- aus
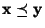 und
und
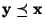 folgt
folgt
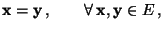
- (d)
-
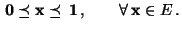
- dass die Update-Funktion
![$ \varphi:E\times(0,1]\to E$](img175.png) isoton
bezüglich der Halbordnung
isoton
bezüglich der Halbordnung 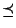 ist, d.h., für beliebige
ist, d.h., für beliebige
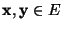 mit
mit
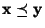 gelte
gelte
- d.h., wir betrachten lediglich eine Folge
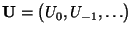 von unabhängigen und
von unabhängigen und
![$ (0,1]$](img167.png) -gleichverteilten Zufallsvariablen und setzen
-gleichverteilten Zufallsvariablen und setzen
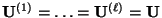 ,
,
- wobei die Markov-Kette
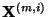 für beliebige
für beliebige
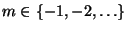 und
und
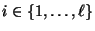 rekursiv
gegeben sei durch
rekursiv
gegeben sei durch