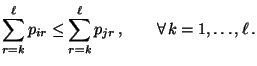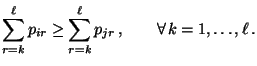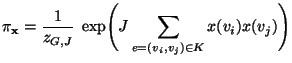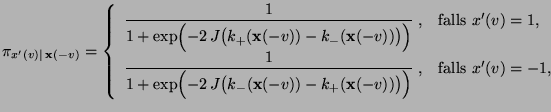- Die in (88) definierte Update-Funktion
![$ \varphi:E\times(0,1]\to E$](img175.png) genügt insbesondere dann der
Isotonie-Bedingung (91),
genügt insbesondere dann der
Isotonie-Bedingung (91),
- wenn der Zustandsraum mit der Menge
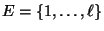 identifiziert wird und dabei die natürliche Ordnung
identifiziert wird und dabei die natürliche Ordnung 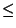 der
Zahlen
der
Zahlen
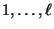 betrachtet wird
betrachtet wird
- und wenn die Simulationsmatrix
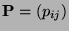 isoton
bezüglich der Ordnung
isoton
bezüglich der Ordnung 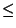 ist, d.h., für beliebige
ist, d.h., für beliebige 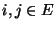 mit
mit 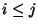 gelte
gelte
- wenn der Zustandsraum mit der Menge
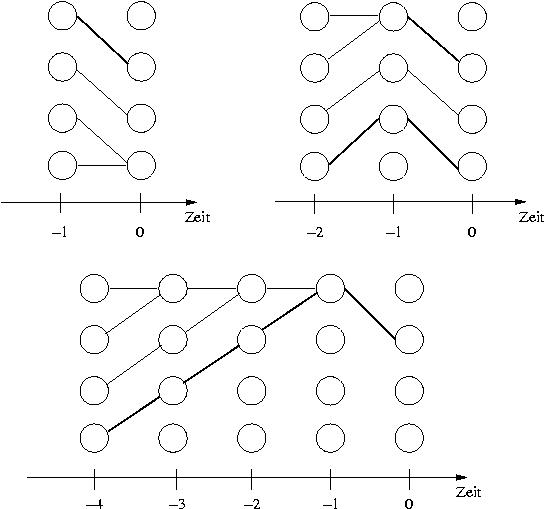
- Eine Klasse von Übergangsmatrizen
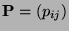 , für die die
Isotonie-Bedingung (100) erfüllt ist, ist durch die
tridiagonalen Matrizen von Geburts- und Todesprozessen
gegeben, so dass
wobei
, für die die
Isotonie-Bedingung (100) erfüllt ist, ist durch die
tridiagonalen Matrizen von Geburts- und Todesprozessen
gegeben, so dass
wobei
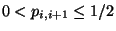 für jedes
für jedes
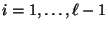 und
und
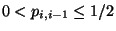 für jedes
für jedes
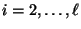 .
.
- Andererseits genügt die in (88) definierte
Update-Funktion
![$ \varphi:E\times(0,1]\to E$](img175.png) der
Antitonie-Bedingung (98),
der
Antitonie-Bedingung (98),
- wenn
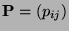 antiton bezüglich der Ordnung
antiton bezüglich der Ordnung 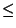 ist,
ist,
- d.h., wenn für beliebige
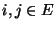 mit
mit 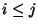
- wenn
- Man kann leicht zeigen, dass es keine tridiagonale Übergangsmatrix
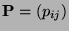 gibt, so dass die Bedingung (101)
erfüllt ist, d.h. Geburts- und Todesprozessen sind niemals
antiton.
gibt, so dass die Bedingung (101)
erfüllt ist, d.h. Geburts- und Todesprozessen sind niemals
antiton.
- Die Antitonie-Bedingung (101) ist jedoch
beispielsweise für die folgende Matrix erfüllt:

- Ähnlich wie bei dem in Abschnitt 3.3.1 diskutierten
Hard-Core-Modell
- betrachten wir einen verbundenen Graph
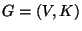 mit der Menge
mit der Menge
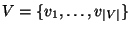 von (endlich vielen) Eckpunkten
von (endlich vielen) Eckpunkten
- und mit einer gewissen Menge
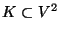 von Kanten
von Kanten
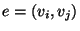 , die jeweils zwei Eckpunkte
, die jeweils zwei Eckpunkte 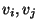 miteinander
verbinden.
miteinander
verbinden.
- betrachten wir einen verbundenen Graph
- Jedem Eckpunkt aus
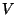 wird entweder der Wert
wird entweder der Wert 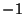 oder
oder 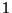 zugeordnet,
zugeordnet,
- wobei der Zustandsraum
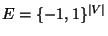 aller Konfigurationen
aller Konfigurationen
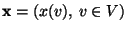 betrachtet wird, d.h., es gilt entweder
betrachtet wird, d.h., es gilt entweder
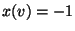 oder
oder 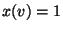 für jedes
für jedes 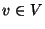
- mit der ,,Bild-Interpretation'', dass
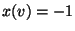 ein weißes Pixel
und
ein weißes Pixel
und 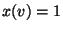 ein schwarzes Pixel bedeutet.
ein schwarzes Pixel bedeutet.
- wobei der Zustandsraum
- Für jedes
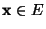 sei die Wahrscheinlichkeit
sei die Wahrscheinlichkeit
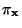 der
Konfiguration
der
Konfiguration
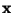 gegeben durch den Ansatz (vgl. auch
Übungsaufgabe 11.1)
gegeben durch den Ansatz (vgl. auch
Übungsaufgabe 11.1)
für einen gewissen Parameter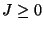 , der in der Physik als
,,inverse Temperatur'' interpretiert wird:
, der in der Physik als
,,inverse Temperatur'' interpretiert wird:
- Für
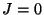 (unendliche Temperatur) ist die in (102)
gegebene Verteilung
(unendliche Temperatur) ist die in (102)
gegebene Verteilung
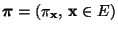 die
(diskrete) Gleichverteilung auf
die
(diskrete) Gleichverteilung auf 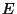 .
.
- Für
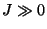 (niedrige Temperatur) besitzen diejenigen
Konfigurationen große Wahrscheinlichkeiten, für die nur wenige
benachbarte (d.h. durch Kanten verbundene) Paare von Eckpunkten
unterschiedlich gefärbt sind.
(niedrige Temperatur) besitzen diejenigen
Konfigurationen große Wahrscheinlichkeiten, für die nur wenige
benachbarte (d.h. durch Kanten verbundene) Paare von Eckpunkten
unterschiedlich gefärbt sind.
- Für
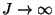 (Null-Temperatur) konvergiert die in
(102) gegebene Verteilung
(Null-Temperatur) konvergiert die in
(102) gegebene Verteilung
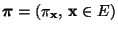 gegen die
,,Zwei-Punkt-Gleicherteilung''
gegen die
,,Zwei-Punkt-Gleicherteilung''
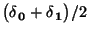 ,
,
- wobei
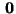 und
und
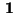 die beiden (extremen) Konfigurationen
sind, die entweder nur aus weißen oder nur aus schwarzen Pixeln
bestehen, d.h.
die beiden (extremen) Konfigurationen
sind, die entweder nur aus weißen oder nur aus schwarzen Pixeln
bestehen, d.h. 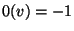 bzw.
bzw. 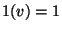 für jedes
für jedes 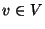 .
.
- Für
- Dabei ist
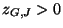 eine (im allgemeinen unbekannte)
Normierungskonstante mit
eine (im allgemeinen unbekannte)
Normierungskonstante mit
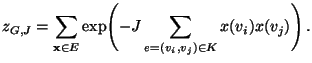
- Die folgenden Abbildungen wurde dem Buch von O. Häggström (2002)
Finite Markov Chains and Algorithmic Applications, CU Press,
Cambridge entnommen.
- Sie verdeutlichen die oben erwähnte Rolle des Parameters
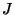 ,
,
- d.h., mit wachsendem
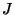 werden die zusammenhängenden ,,Klumpen''
von jeweils identisch gefärbten Pixeln größer.
werden die zusammenhängenden ,,Klumpen''
von jeweils identisch gefärbten Pixeln größer.
Abbildung: Typische Konfigurationen des Ising-Models für 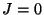 (oben
links),
(oben
links), 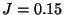 (oben rechts),
(oben rechts), 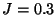 (unten links) bzw.
(unten links) bzw.  (unten rechts)
(unten rechts)
- Sie verdeutlichen die oben erwähnte Rolle des Parameters
- Die Simulationsmatrix
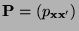 sei durch
den Gibbs-Sampler gegeben. Es gelte also (36), d.h.
sei durch
den Gibbs-Sampler gegeben. Es gelte also (36), d.h.
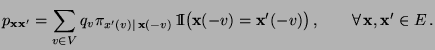
- Dabei gilt für beliebige
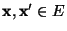 mit
mit
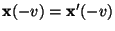 wobei
wobei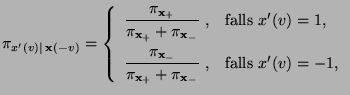
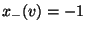 und
und
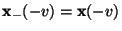 bzw.
bzw. 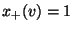 und
und
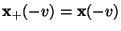 .
.
- Aus (102) ergibt sich somit für
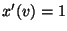 und analog für
und analog für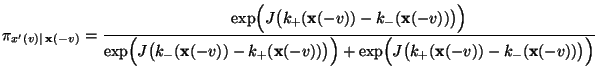
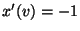 bzw.
bzw.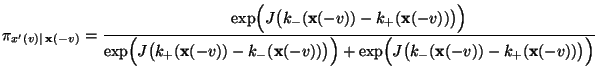
wobei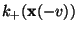 bzw.
bzw.
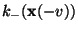 die Anzahl
derjenigen mit
die Anzahl
derjenigen mit 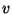 verbundenen Eckpunkte ist, die auf
verbundenen Eckpunkte ist, die auf 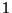 bzw.
bzw.
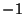 gesetzt sind.
gesetzt sind.
- Dabei gilt für beliebige
- Für den Zustandsraum
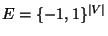 definieren wir nun die
Halbordnungsrelation
definieren wir nun die
Halbordnungsrelation 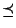
- mit
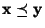 , falls
, falls
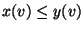 für jedes
für jedes 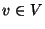 ,
so dass
,
so dass
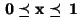 für jedes
für jedes
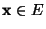 ,
,
- wobei die Elemente des Zustandsraumes
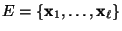 so numeriert sein mögen, dass
so numeriert sein mögen, dass
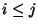 gilt, falls
gilt, falls
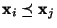 (was beispielsweise
bei der lexikographischen Numierung der Elemente von
(was beispielsweise
bei der lexikographischen Numierung der Elemente von 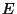 zutreffend ist).
zutreffend ist).
- mit
- Aus (103) ergibt sich dann, dass für beliebige
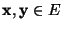 mit
mit
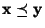
weil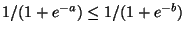 für beliebige Zahlen
für beliebige Zahlen
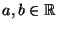 mit
mit 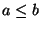 .
.
- Die Update-Funktion
![$ \varphi:E\times(0,1]^2\to E$](img2110.png) sei gegeben
durch
sei gegeben
durch
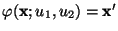 , wobei
, wobei
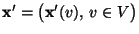 und für jedes
und für jedes
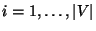
![$\displaystyle {\mathbf{x}}^\prime(v_i)=\left\{\begin{array}{ll} 1\,,&\mbox{fall...
...x}}(-v_i)}$,}\\ [3\jot]
{\mathbf{x}}(v_i)\,,&\mbox{sonst.}
\end{array}\right.
$](img2113.png)