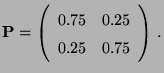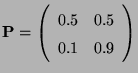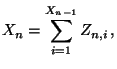(vgl. O. Häggström (2002) Finite Markov Chains and Algorithmic Applications. CU Press, Cambridge)
- Wir betrachten zunächst Regionen, in denen sich typischerweise
längere Regen- bzw. Trockenperioden abwechseln, wobei Regentage
bzw. Sonnentage im Mittel etwa gleich oft vorkommen.
- Dann ist es relativ einfach, das Wetter des folgenden Tages
vorherzusagen, falls dabei nur die beiden ,,Zustände''
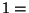 ,,Regen'' bzw.
,,Regen'' bzw. 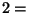 ,,Sonnenschein'' betrachtet werden.
,,Sonnenschein'' betrachtet werden.
- Wenn wir annehmen, dass die Prognose in 75% aller Fälle richtig ist (und zwar unabhängig davon, ob es zum gegenwärtigen Tag regnet oder die Sonne scheint),
- dann kann die Wettervorhersage durch eine Markov-Kette mit der
folgenden Übergangsmatrix modelliert werden:
- Dann ist es relativ einfach, das Wetter des folgenden Tages
vorherzusagen, falls dabei nur die beiden ,,Zustände''
- In Regionen, in denen diese Symmetrie zwischen ,,Regen'' bzw.
,,Sonnenschein'' nicht vorliegt, sondern Sonnentage wesentlich
öfter als Regentage vorkommen, sollte
- die Wettervorhersage nicht durch die in (7) betrachtete Übergangsmatrix modelliert werden.
- In diesem Fall könnte beispielsweise die Übergangsmatrix
ein geeignetes Modell sein.
- Klassische Beispiele für Markov-Ketten sind durch sogenannte zufällige Irrfahrten gegeben, die auch in der deutschsprachigen
Literatur Random Walk genannt werden, wobei das
(unbeschränkte) Basismodell auf die folgende Weise gegeben ist.
- Sei
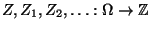 eine Folge von unabhängigen
und identisch verteilten Zufallsvariablen, die nur Werte in der
Menge
eine Folge von unabhängigen
und identisch verteilten Zufallsvariablen, die nur Werte in der
Menge
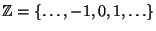 der ganzen Zahlen annehmen.
der ganzen Zahlen annehmen.
- Sei
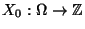 eine beliebige Zufallsvariable, die von den
,,Zuwächsen''
eine beliebige Zufallsvariable, die von den
,,Zuwächsen''
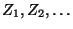 unabhängig ist, und sei
unabhängig ist, und sei
- Dann bilden die Zufallsvariablen
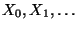 eine
Markov-Kette mit dem (abzählbar unendlichen) Zustandsraum
eine
Markov-Kette mit dem (abzählbar unendlichen) Zustandsraum
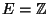 ,
mit der Anfangsverteilung
,
mit der Anfangsverteilung
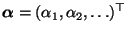 , wobei
, wobei
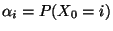 , und mit den Übergangswahrscheinlichkeiten
, und mit den Übergangswahrscheinlichkeiten
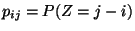 .
.
- Sei
- Beachte
- Durch die in (9) gegebene Markov-Kette kann die
Risikoreserve von versicherungs- bzw. finanztechnischen
Bilanzierungprozessen modelliert werden, wobei
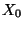 als
(zufällige) Anfangsreserve aufgefasst wird und der ,,Zuwachs''
als
(zufällige) Anfangsreserve aufgefasst wird und der ,,Zuwachs''
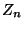 beispielsweise die Differenz
beispielsweise die Differenz
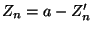 aus
risikofreien Einnahmen
aus
risikofreien Einnahmen 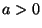 und zufallsbedingten
Ausgaben/Verlusten
und zufallsbedingten
Ausgaben/Verlusten
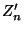 sein kann.
sein kann.
- Ein anderer Spezialfall ist das bereits in Abschnitt WR-1.3
betrachtete Beispiel des zufälligen Gesamtgewinns
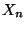 aus
aus 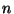 Roulette-Spielen, bei dem
Roulette-Spielen, bei dem 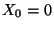 angenommen wird und
angenommen wird und
- die Verteilung des zufälligen ,,Zuwachses''
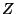 für jedes einzelne
Spiel durch
für jedes einzelne
Spiel durch
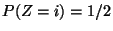 für
für 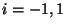 und
und 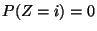 für
für
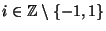 gegeben ist.
gegeben ist.
- Durch die in (9) gegebene Markov-Kette kann die
Risikoreserve von versicherungs- bzw. finanztechnischen
Bilanzierungprozessen modelliert werden, wobei
- Die Anzahl der Kunden, die vor einer beliebigen, jedoch fest
vorgegebenen Kasse eines Supermarktes warten, lässt sich wie folgt
durch eine Markov-Kette modellieren.
- Sei
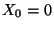 die Anzahl der Kunden, die bei Öffnung des
Supermarktes vor der Kasse warten.
die Anzahl der Kunden, die bei Öffnung des
Supermarktes vor der Kasse warten.
- Mit
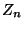 bezeichnen wir die zufällige Anzahl derjenigen Kunden,
die sich vor der Kasse anstellen, während der
bezeichnen wir die zufällige Anzahl derjenigen Kunden,
die sich vor der Kasse anstellen, während der 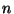 -te Kunde bedient
wird;
-te Kunde bedient
wird;
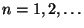 .
.
- Dabei setzen wir voraus, dass die Zufallsvariablen
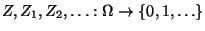 unabhängig und
identisch verteilt sind.
unabhängig und
identisch verteilt sind.
- Sei
- Die rekursiv definierte Folge
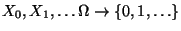 von Zufallsvariablen mit
von Zufallsvariablen mit
bildet dann eine Markov-Kette, deren Übergangsmatrix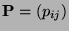 gegeben ist durch
gegeben ist durch
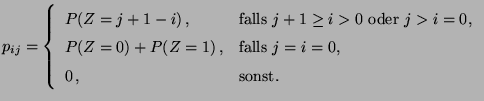
- Dabei ist
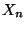 die zufällige Anzahl von Kunden in der
Warteschlange, unmittelbar nachdem die Bedienung des
die zufällige Anzahl von Kunden in der
Warteschlange, unmittelbar nachdem die Bedienung des
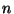 -ten Kunden beendet wurde (d.h. ohne die Berücksichtigung
desjenigen Kunden, mit dessen Bedienung gegebenenfalls gerade
begonnen wurde und der die Warteschlange deshalb bereits verlassen
hat).
-ten Kunden beendet wurde (d.h. ohne die Berücksichtigung
desjenigen Kunden, mit dessen Bedienung gegebenenfalls gerade
begonnen wurde und der die Warteschlange deshalb bereits verlassen
hat).
- Wir betrachten den Fortpflanzungsprozess einer bestimmten
Population, wobei
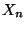 die (zufällige) Gesamtanzahl der
Nachkommen in der
die (zufällige) Gesamtanzahl der
Nachkommen in der 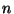 -ten Generation sei;
-ten Generation sei; 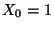 .
.
- Wir nehmen an, dass
wobei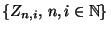 eine Familie von unabhängigen und
identisch verteilten Zufallsvariaben ist, die ihre Werte in der
Menge
eine Familie von unabhängigen und
identisch verteilten Zufallsvariaben ist, die ihre Werte in der
Menge
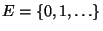 annehmen.
annehmen.
- Die Zufallsvariable
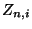 ist dabei die zufällige Anzahl der
(unmittelbaren) Nachkommen des
ist dabei die zufällige Anzahl der
(unmittelbaren) Nachkommen des 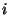 -ten Individuums der
-ten Individuums der 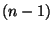 -ten
Generation.
-ten
Generation.
- Die Folge
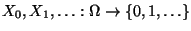 von
Zufallsvariablen, die durch
von
Zufallsvariablen, die durch 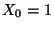 und durch die
Rekursionsgleichung (11) gegeben ist, wird Verzweigungsprozess genannt.
und durch die
Rekursionsgleichung (11) gegeben ist, wird Verzweigungsprozess genannt.
- Man kann zeigen (vgl. Abschnitt 2.1.3), dass
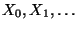 eine Markov-Kette ist mit den
Übergangswahrscheinlichkeiten
eine Markov-Kette ist mit den
Übergangswahrscheinlichkeiten
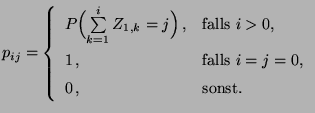
- Weitere Beispiele von Markov-Ketten können wie folgt konstruiert
werden (vgl. E. Behrends (2000) Introduction to Markov
Chains. Vieweg, Braunschweig, S.4).
- Wir betrachten den endlichen Zustandsraum
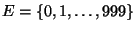 ,
die Anfangsverteilung
,
die Anfangsverteilung
und die Übergangswahrscheinlichkeiten![$\displaystyle p_{ij}=\left\{\begin{array}{ll} \displaystyle\frac{1}{6}\;, &
\mb...
...od(1000)\in\{1,\ldots,6\}$,}\\ [3\jot]
0\,, &\mbox{sonst.}
\end{array}\right.
$](img116.png)
- Seien
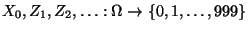 unabhängige
Zufallsvariablen, wobei die Verteilung von
unabhängige
Zufallsvariablen, wobei die Verteilung von 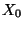 durch
(12) gegeben sei und
durch
(12) gegeben sei und
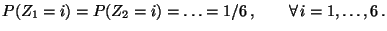
- Die rekursiv definierte Folge
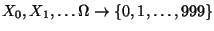 von Zufallsvariablen
mit
von Zufallsvariablen
mit
für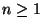 bildet dann eine Markov-Kette, die zyklischer
Random Walk genannt wird; vgl. auch Übungsaufgabe 1.3.
bildet dann eine Markov-Kette, die zyklischer
Random Walk genannt wird; vgl. auch Übungsaufgabe 1.3.
- Wir betrachten den endlichen Zustandsraum
- Beachte
- Dieses Modell einer Markov-Kette kann auf die folgende Weise experimentell realisiert werden: Wir werfen zunächst
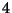 -mal eine
Münze und registrieren, wie oft dabei das Ereignis ,,Zahl''
eintritt. Die Anzahl
-mal eine
Münze und registrieren, wie oft dabei das Ereignis ,,Zahl''
eintritt. Die Anzahl 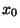 dieser Ereignisse fassen wir als
Realisierung des zufälligen Anfangszustandes
dieser Ereignisse fassen wir als
Realisierung des zufälligen Anfangszustandes 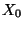 auf; vgl. das
Bernoulli-Schema in Abschnitt WR-3.2.1.
auf; vgl. das
Bernoulli-Schema in Abschnitt WR-3.2.1.
- Danach werfen wir
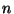 -mal einen Würfel und registrieren die
jeweiligen Augenzahlen. Die Augenzahl
-mal einen Würfel und registrieren die
jeweiligen Augenzahlen. Die Augenzahl 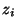 , die beim
, die beim 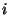 -ten Wurf
des Würfels eintritt, fassen wir als Realisierung des zufälligen
,,Zuwachses''
-ten Wurf
des Würfels eintritt, fassen wir als Realisierung des zufälligen
,,Zuwachses'' 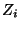 auf;
auf;
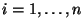 .
.
- Der neue ,,Systemzustand''
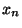 ergibt sich dann durch die
,,Aktualisierung'' des alten Systemzustandes
ergibt sich dann durch die
,,Aktualisierung'' des alten Systemzustandes 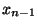 gemäß (13), und zwar unter Berücksichtigung des
,,Zuwachses''
gemäß (13), und zwar unter Berücksichtigung des
,,Zuwachses'' 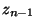 .
.
- Wenn das Experiment nicht tatsächlich durch das Werfen einer Münze
bzw. eines Würfels, sondern durch die Erzeugung entsprechender
Pseudozufallszahlen
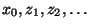 mit dem Computer
durchgeführt wird, dann spricht man von Monte-Carlo-Simulation.
mit dem Computer
durchgeführt wird, dann spricht man von Monte-Carlo-Simulation.
- Methoden zur Konstruktion von dynamischen Simulationsalgorithmen, die auf Markov-Ketten beruhen, werden im zweiten Teil der Vorlesung ausführlich behandelt.
- Dieses Modell einer Markov-Kette kann auf die folgende Weise experimentell realisiert werden: Wir werfen zunächst