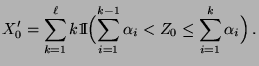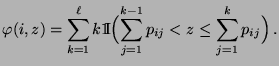Nächste Seite: Matrix der -stufigen Übergangswahrscheinlichkeiten
Aufwärts: Modellbeschreibung und Beispiele
Vorherige Seite: Beispiele
Inhalt
Rekursive Darstellung
- In diesem Abschnitt zeigen wir,
- wie sich Markov-Ketten aus Folgen von unabhängigen und identisch
verteilten Zufallsvariablen konstruieren lassen,
- dass somit die Rekursionsformeln (9),
(10), (11) und (13)
Spezialfälle eines allgemeinen Konstruktionsprinzips für
Markov-Ketten sind
- und dass auch umgekehrt jede Markov-Kette als Lösung einer
rekursiven stochastischen Gleichung aufgefasst werden kann.
- So wie bisher sei
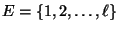 eine endliche (oder
abzählbar unendliche) Menge.
eine endliche (oder
abzählbar unendliche) Menge.
- Beweis
-
- Beachte
-
Wir zeigen nun, dass sich auch umgekehrt jede Markov-Kette als
Lösung einer rekursiven stochastischen Gleichung auffassen lässt.
- Sei
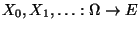 eine beliebige Markov-Kette mit
dem Zustandsraum
eine beliebige Markov-Kette mit
dem Zustandsraum
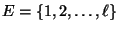 , der Anfangsverteilung
, der Anfangsverteilung
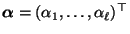 und der
Übergangsmatrix
und der
Übergangsmatrix
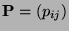 .
.
- Mit Hilfe einer Rekursionsgleichung, die die gleiche Form wie
(14) hat, wird eine Markov-Kette
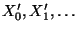 mit (vorgegebener)
Anfangsverteilung
mit (vorgegebener)
Anfangsverteilung
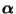 und Übergangsmatrix
und Übergangsmatrix
 rekursiv
konstruiert, so dass
rekursiv
konstruiert, so dass
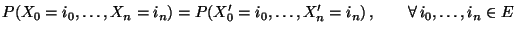 |
(16) |
für jedes 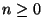 gilt:
gilt:
- Wir gehen von einer Folge
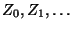 von unabhängigen und
identisch auf
von unabhängigen und
identisch auf ![$ (0,1]$](img167.png) -gleichverteilten Zufallsvariablen aus.
-gleichverteilten Zufallsvariablen aus.
- Zunächst wird die
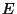 -wertige Zufallsvariable
-wertige Zufallsvariable
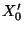 wie
folgt definiert:
wie
folgt definiert:
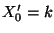
genau dann, wenn
![$\displaystyle \qquad
Z_0\in\Bigl(\sum_{i=1}^{k-1}
\alpha_i,\sum_{i=1}^{k}\alpha_i\Bigr]\,,
$](img170.png)
für jedes
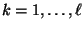 , d.h.,
, d.h.,
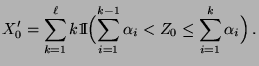 |
(17) |
- Die Zufallsvariablen
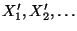 werden dann
rekursiv definiert: Und zwar setzen wir
werden dann
rekursiv definiert: Und zwar setzen wir
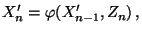 |
(18) |
wobei die Funktion
![$ \varphi:E\times(0,1]\to E$](img175.png) gegeben ist durch
gegeben ist durch
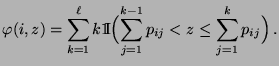 |
(19) |
- Man kann sich leicht überlegen, dass die Wahrscheinlichkeiten
 für die
in (17)-(18) rekursiv definierte
Folge
für die
in (17)-(18) rekursiv definierte
Folge
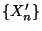 durch (3) gegeben sind,
d.h.,
durch (3) gegeben sind,
d.h.,
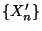 ist eine Markov-Kette mit der
Anfangsverteilung
ist eine Markov-Kette mit der
Anfangsverteilung
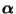 und der Übergangsmatrix
und der Übergangsmatrix
 ,
vgl. Übungsaufgabe 2.1.
,
vgl. Übungsaufgabe 2.1.
- Beachte
-
- Folgen von Zufallsvariablen
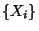 and
and
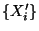 , für die (16)
gilt, werden stochastisch äquivalent genannt.
, für die (16)
gilt, werden stochastisch äquivalent genannt.
- Das in (17)-(19) gegebene
Konstruktionsprinzip kann zur Monte-Carlo-Simulation von
Markov-Ketten mit vorgegebener Anfangsverteilung und
Übergangsmatrix genutzt werden.
- Markov-Ketten mit abzählbar unendlichem Zustandsraum können auf
die gleiche Weise konstruiert bzw. simuliert werden, wobei dann in
(17)-(19) lediglich die Komponenten
bzw. Eintragungen von unendlich dimensionalen Vektoren
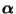 bzw. Matrizen
bzw. Matrizen
 betrachtet werden müssen.
betrachtet werden müssen.




Nächste Seite: Matrix der -stufigen Übergangswahrscheinlichkeiten
Aufwärts: Modellbeschreibung und Beispiele
Vorherige Seite: Beispiele
Inhalt
Ursa Pantle
2003-09-29
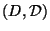 ein beliebiger Maßraum, beispielsweise
ein beliebiger Maßraum, beispielsweise
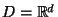 der
der 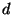 -dimensionale euklidische Raum und
-dimensionale euklidische Raum und
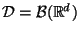 die
die 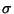 -Algebra der Borel-Mengen in
-Algebra der Borel-Mengen in
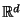 , oder
, oder ![$ D=[0,1]$](img137.png) das Einheitsintervall und
das Einheitsintervall und
![$ \mathcal{D}=\mathcal{B}([0,1])$](img138.png) die
die 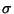 -Algebra der Borel-Mengen in
-Algebra der Borel-Mengen in
![$ [0,1]$](img139.png) .
.
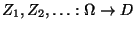 eine Folge von unabhängigen
und identisch verteilten Zufallsvariablen, die ihre Werte in
eine Folge von unabhängigen
und identisch verteilten Zufallsvariablen, die ihre Werte in 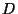 annehmen, und die Zufallsvariable
annehmen, und die Zufallsvariable
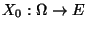 sei unabhängig
von
sei unabhängig
von
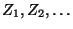 .
.
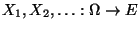 seien durch die
stochastische Rekursionsgleichung
seien durch die
stochastische Rekursionsgleichung
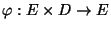 eine beliebige (messbare)
Funktion ist.
eine beliebige (messbare)
Funktion ist.
![$\displaystyle \qquad
Z_0\in\Bigl(\sum_{i=1}^{k-1}
\alpha_i,\sum_{i=1}^{k}\alpha_i\Bigr]\,,
$](img170.png)