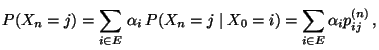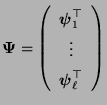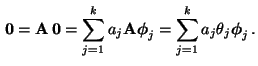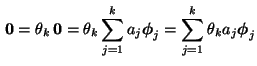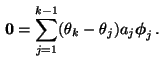Nächste Seite: Ergodizität und Stationarität
Aufwärts: Modellbeschreibung und Beispiele
Vorherige Seite: Rekursive Darstellung
Inhalt
Matrix der 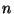 -stufigen Übergangswahrscheinlichkeiten
-stufigen Übergangswahrscheinlichkeiten
- Beachte
-
- Die Matrix
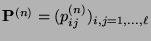 wird
die
wird
die 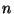 -stufige Übergangsmatrix der Markov-Kette
-stufige Übergangsmatrix der Markov-Kette 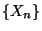 genannt.
genannt.
- Mit der Schreibweise
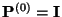 , wobei
, wobei
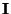 die
die
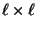 -dimensionale Einheitsmatrix bezeichnet, lassen
sich die folgenden Darstellungsformeln für
-dimensionale Einheitsmatrix bezeichnet, lassen
sich die folgenden Darstellungsformeln für
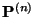 angeben.
angeben.
Lemma 2.1
Für beliebige
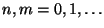
gilt
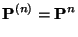 |
(22) |
und somit
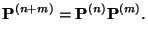 |
(23) |
- Beweis
 Die Gleichung (22) folgt
unmittelbar aus (20) und aus der Definition der
Matrix-Multiplikation.
Die Gleichung (22) folgt
unmittelbar aus (20) und aus der Definition der
Matrix-Multiplikation.

- Beispiel
 (Wettervorhersage)
(Wettervorhersage)
- Sei
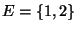 , und sei
eine beliebige Übergangsmatrix mit
, und sei
eine beliebige Übergangsmatrix mit
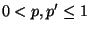 .
.
- Man kann zeigen (vgl. Übungsaufgabe 2.3), dass dann die
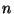 -stufige Übergangsmatrix
-stufige Übergangsmatrix
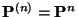 gegeben ist
durch
gegeben ist
durch
- Beachte
-
- Die Matrix-Identität (23) wird in der Literatur
Gleichung von Chapman-Kolmogorov genannt.
- Unmittelbar aus (23) ergeben sich die folgenden
nützlichen Abschätzungen.
Außerdem ergibt sich aus Lemma 2.1 die folgende
Darstellung der Verteilung des zufälligen Zustandes 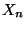 der
Markov-Kette zum Zeitpunkt
der
Markov-Kette zum Zeitpunkt 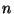 .
.
- Beweis
-
- Aus der Formel der totalen Wahrscheinlichkeit (vgl.
Theorem WR-2.6) und aus (21) folgt, dass
wobei wir
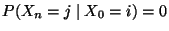 setzen, falls
setzen, falls
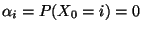 .
.
- Die Behauptung (26) ergibt sich nun aus
Lemma 2.1.

- Beachte
-
- Wegen Theorem 2.3 kann die Berechnung der
Wahrscheinlichkeiten
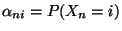 auf die Berechnung der
auf die Berechnung der
 -ten Potenz
-ten Potenz
 der Übergangsmatrix
der Übergangsmatrix
 zurückgeführt
werden.
zurückgeführt
werden.
- Dabei ist in vielen Fällen die sogenannte Spektraldarstellung von
 nützlich, die auf die folgende
Weise mit Hilfe der Eigenwerte bzw. Eigenvektoren der
Übergangsmatrix
nützlich, die auf die folgende
Weise mit Hilfe der Eigenwerte bzw. Eigenvektoren der
Übergangsmatrix
 bestimmt werden kann.
bestimmt werden kann.
- Zur Erinnerung
- Sei
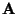 eine (nicht notwendig stochastische)
eine (nicht notwendig stochastische)
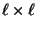 Matrix, seien
Matrix, seien
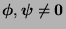 zwei
zwei
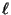 -dimensionale (Spalten-) Vektoren, so daß jeweils mindestens
eine ihrer Komponenten von 0 verschieden ist, und sei
-dimensionale (Spalten-) Vektoren, so daß jeweils mindestens
eine ihrer Komponenten von 0 verschieden ist, und sei 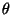 eine beliebige (reelle oder komplexe) Zahl.
eine beliebige (reelle oder komplexe) Zahl.
- Falls
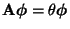 bzw. bzw. |
(27) |
dann ist 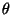 ein Eigenwert von
ein Eigenwert von
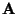 , und
, und
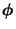 bzw.
bzw.
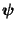 ist ein rechter bzw. linker (zu
ist ein rechter bzw. linker (zu 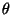 gehörender) Eigenvektor.
gehörender) Eigenvektor.
- Weil (27) und
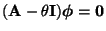
bzw.
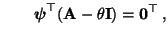
äquivalent sind, ist 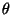 genau dann ein Eigenwert von
genau dann ein Eigenwert von
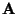 , wenn
, wenn 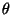 eine Lösung der sogenannten charakteristischen Gleichung ist:
eine Lösung der sogenannten charakteristischen Gleichung ist:
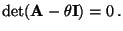 |
(28) |
- Weil (28) eine algebraische Gleichung der Ordnung
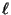 ist, besitzt sie somit
ist, besitzt sie somit 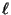 Lösungen
Lösungen
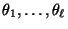 , die komplex sein können und die
nicht alle voneinander verschieden sein müssen.
, die komplex sein können und die
nicht alle voneinander verschieden sein müssen.
- Wir nehmen o.B.d.A. an, dass die Eigenwerte
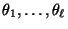 so numeriert sind, dass
so numeriert sind, dass
- Für jeden Eigenwert
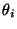 existieren (jeweils von
existieren (jeweils von 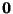 verschiedene) rechte bzw. linke Eigenvektoren
verschiedene) rechte bzw. linke Eigenvektoren
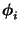 bzw.
bzw.
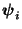 .
.
- Sei
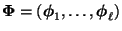 die
die
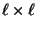 Matrix, die aus den rechten Eigenvektoren
Matrix, die aus den rechten Eigenvektoren
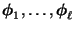 besteht, und sei
die
besteht, und sei
die
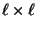 Matrix, die aus den linken Eigenvektoren
Matrix, die aus den linken Eigenvektoren
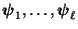 gebildet wird.
gebildet wird.
- Mit dieser Schreibweise ergibt sich, dass
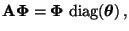 |
(29) |
wobei
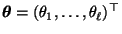 und
und
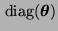 die Diagonalmatrix mit den Diagonalelementen
die Diagonalmatrix mit den Diagonalelementen
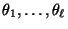 bezeichnet.
bezeichnet.
- Falls die Eigenvektoren
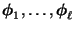 linear
unabhängig sind,
linear
unabhängig sind,
- dann existiert die inverse Matrix
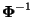 , und wir können
, und wir können
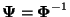 setzen.
setzen.
- Außerdem ergibt sich in diesem Fall aus (29), dass
und somit
- Hieraus ergibt sich die Spektraldarstellung von
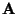 :
:
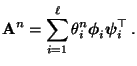 |
(30) |
- Beachte
-
- Die Anwendung von (30) für die Übergangsmatrix
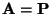 führt zu einem einfachen Algorithmus zur Berechnung
der
führt zu einem einfachen Algorithmus zur Berechnung
der 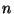 -ten Potenz
-ten Potenz
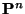 in (26).
in (26).
- Dabei sind lediglich die Eigenwerte und Eigenvektoren von
 zu berechnen, wofür Standard-Software wie MAPLE, MATLAB oder
MATHEMATICA verwendet werden kann.
zu berechnen, wofür Standard-Software wie MAPLE, MATLAB oder
MATHEMATICA verwendet werden kann.
- Ein wesentlicher Vorteil der Spektraldarstellung (30)
besteht darin, dass sich bei der Verwendung von (30)
die Komplexität der numerischen Berechnung von
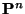 mit
wachsendem
mit
wachsendem 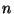 nicht erhöht.
nicht erhöht.
- Allerdings wird bei der Herleitung von (30)
vorausgesetzt, dass die Eigenvektoren
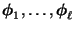 linear unabhängig sind. Das
folgende Lemma liefert eine hinreichende Bedingung hierfür.
linear unabhängig sind. Das
folgende Lemma liefert eine hinreichende Bedingung hierfür.
- Beweis
-
- Die Gültigkeit der ersten Teilaussage zeigen wir mit vollständiger
Induktion.
- Weil jeder Eigenvektor
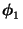 mindestens eine Komponente hat,
die von 0 verschieden ist, impliziert
mindestens eine Komponente hat,
die von 0 verschieden ist, impliziert
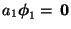 ,
dass
,
dass 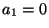 .
.
- Seien nun sämtliche Eigenwerte
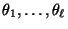 von
von
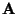 voneinander verschieden, und für ein gewisses
voneinander verschieden, und für ein gewisses 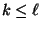 seien die Eigenvetoren
seien die Eigenvetoren
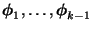 linear
unabhängig.
linear
unabhängig.
- Um zu beweisen, dass dann auch die Eigenvektoren
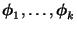 linear unabhängig sind, genügt es zu
zeigen, dass
linear unabhängig sind, genügt es zu
zeigen, dass
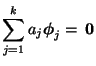 |
(32) |
die Gültigkeit von
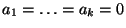 impliziert.
impliziert.
- Die Koeffizienten
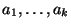 seien nun so gewählt, dass
(32) gilt. Dann gilt auch
seien nun so gewählt, dass
(32) gilt. Dann gilt auch
- Auf die gleiche Weise ergibt sich, dass
und somit
- Weil angenommen wird, dass die Eigenvektoren
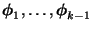 linear unabhängig sind, folgt
hieraus, dass
bzw.
linear unabhängig sind, folgt
hieraus, dass
bzw.
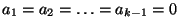 , weil
, weil
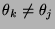 für
für
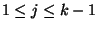 .
.
- Wegen (32) muss dann auch
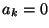 gelten.
gelten.
- Falls sämtliche Eigenwerte
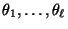 von
von
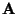 voneinander verschieden sind,
voneinander verschieden sind,
- dann besteht also die
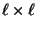 Matrix
Matrix
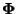 aus
aus 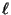 linear unabhängigen Spaltenvektoren,
linear unabhängigen Spaltenvektoren,
- und
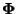 ist somit invertierbar.
ist somit invertierbar.
- Die Matrix
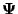 der linken Eigenvektoren kann also durch den
Ansatz
der linken Eigenvektoren kann also durch den
Ansatz
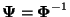 gebildet werden, woraus sich
unmittelbar die Gültigkeit von (31) ergibt.
gebildet werden, woraus sich
unmittelbar die Gültigkeit von (31) ergibt.





Nächste Seite: Ergodizität und Stationarität
Aufwärts: Modellbeschreibung und Beispiele
Vorherige Seite: Rekursive Darstellung
Inhalt
Ursa Pantle
2003-09-29
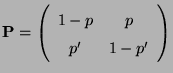
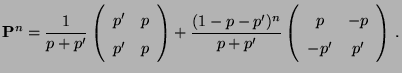
![]() der
Markov-Kette zum Zeitpunkt
der
Markov-Kette zum Zeitpunkt ![]() .
.