- Die Stichprobenwerte
 werden manchmal auch als
Urliste bzw. als Roh- oder Primärdaten bezeichnet.
werden manchmal auch als
Urliste bzw. als Roh- oder Primärdaten bezeichnet.
- Weil die direkte Auflistung der Rohdaten
 mit
wachsendem Stichprobenumfang
mit
wachsendem Stichprobenumfang 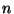 schnell unübersichtlich wird, ist
es manchmal zweckmäßig bzw. notwendig, die Rohdaten in einer
anderen Form darzustellen.
schnell unübersichtlich wird, ist
es manchmal zweckmäßig bzw. notwendig, die Rohdaten in einer
anderen Form darzustellen.
- So kann es beispielsweise bei diskreten
Merkmalen/Kenngrößen/Variablen sinnvoll sein, anstelle der
Rohdaten
 zunächst
zunächst
- die Folge der vorhandenen bzw. potentiell möglichen
Ausprägungen/Werte
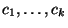 (ohne Berücksichtigung
eventuell vorkommender Wiederholungen) zu betrachten und der Größe
nach zu ordnen, d.h.
(ohne Berücksichtigung
eventuell vorkommender Wiederholungen) zu betrachten und der Größe
nach zu ordnen, d.h.
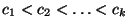 , und dann
, und dann
- für jedes
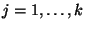 die absolute Häufigkeit
die absolute Häufigkeit
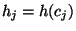 bzw. die relative Häufigkeit
bzw. die relative Häufigkeit 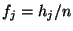 der
Ausprägung
der
Ausprägung 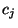 zu bestimmen.
zu bestimmen.
- die Folge der vorhandenen bzw. potentiell möglichen
Ausprägungen/Werte
- Beispiel
- Wir betrachten die Anzahlen
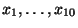 kariöser Zähne von
10 Schülern, wobei
kariöser Zähne von
10 Schülern, wobei
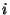
1 2 3 4 5 6 7 8 9 10 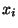
5 1 1 0 5 1 0 2 0 0 - Dann ergeben sich die folgenden absoluten bzw. relativen
Häufigkeiten der Ausprägungen
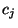 :
:
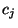
0 1 2 3 4 5 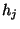
4 3 1 0 0 2 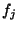
0.4 0.3 0.1 0 0 0.2
- Wir betrachten die Anzahlen
- Beachte
- Wenn der Stichprobenumfang
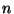 groß ist, dann ist die Menge
groß ist, dann ist die Menge
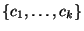 der überhaupt vorhandenen bzw. potentiell
möglichen Ausprägungen/Werte typischerweise deutlich kleiner (und
damit wesentlich übersichtlicher) als die Menge der Rohdaten
der überhaupt vorhandenen bzw. potentiell
möglichen Ausprägungen/Werte typischerweise deutlich kleiner (und
damit wesentlich übersichtlicher) als die Menge der Rohdaten
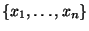 .
.
- Bei stetigen bzw. quasi-stetigen Merkmalen/Kenngrößen/Variablen können ebenfalls absolute bzw. relative Häufigkeiten betrachtet werden, wenn die Rohdaten vorher auf geeignete Weise zu Klassen zusammengefasst und die Häufigkeiten dann für die gruppierten Daten bestimmt werden.
- Dabei ist jedoch zu beachten, dass die Gruppierung/Aggregation von Daten stets mit einem Informationsverlust verbunden ist.
- Wenn der Stichprobenumfang
- Wir betrachten nun Merkmale/Kenngrößen/Variablen, die zumindest
ordinalskaliert sind, und zerlegen die (reelle) Zahlengerade
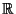 in
in 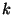 Intervalle
Intervalle 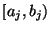 , die sich unmittelbar aneinander
anschließen, d.h.
, die sich unmittelbar aneinander
anschließen, d.h.
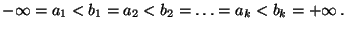
- Für jedes
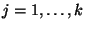 betrachten wir die absolute Häufigkeit
betrachten wir die absolute Häufigkeit
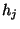 bzw. die relative Häufigkeit
bzw. die relative Häufigkeit 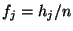 derjenigen
Stichprobenwerte
derjenigen
Stichprobenwerte
 , die in das Intervall
, die in das Intervall
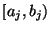 fallen.
fallen.
- Ein Histogramm ist ein Säulendiagramm, wobei den Klassen
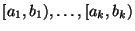 Säulen zugeordnet werden,
deren Flächeninhalte jeweils gleich oder proportional zu den
absoluten bzw. relativen Häufigkeiten
Säulen zugeordnet werden,
deren Flächeninhalte jeweils gleich oder proportional zu den
absoluten bzw. relativen Häufigkeiten
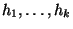 bzw.
bzw.
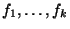 sind.
sind.
- Beispiel
- Für den obenbetrachteten Datensatz der Anzahlen kariöser Zähne bei
einer Gruppe von 10 Schülern besteht keine Notwendigkeit, die 6
beobachteten Werte
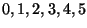 zu einer kleineren Anzahl von
Klassen zusammenzufassen.
zu einer kleineren Anzahl von
Klassen zusammenzufassen.
- Um ein Säulendiagramm zu erhalten, werden dennoch die
,,Intervall-Klassen''
betrachtet, wobei diese Zerlegung der Zahlengerade
![$\displaystyle [-\infty,1),[1,2),\ldots, [4,5),[5,,\infty]
$](img195.png)
 zu den
(bereits obenerwähnten) absoluten Häufigkeiten
zu den
(bereits obenerwähnten) absoluten Häufigkeiten
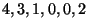 führt.
führt.
- Hieraus ergibt sich das folgende Histogramm:
![\includegraphics[width=13cm]{histogramm.eps}](img197.png)
- Für den obenbetrachteten Datensatz der Anzahlen kariöser Zähne bei
einer Gruppe von 10 Schülern besteht keine Notwendigkeit, die 6
beobachteten Werte