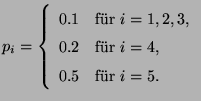Next: Absolute und relative Häufigkeiten;
Up: Kenngrößen zur Beschreibung von
Previous: Maßzahlen für die Streuung
Contents
Konzentrationsmaße
Wir betrachten nun die folgenden beiden Charakteristiken zur
Beschreibung von univariaten Daten, die in der Literatur Konzentrationsmaße genannt werden.
- Lorenzkurve
- Gini-Koeffizient
- Weil sich die Stärke der Konzentration durch die Entfernung der
Lorenzkurve von der NO-Diagonalen ausdrücken lässt, ist es
naheliegend, in die Definition eines weiteren Konzentrationsmaßes
die Fläche zwischen der Lorenzkurve und der NO-Diagonalen
einzubeziehen.
- Dabei betrachtet man den Quotienten dieses Flächeninhaltes zum
,,Gesamtflächeninhalt'' des rechtwinkligen Dreiecks, das durch die
Punkte
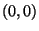 ,
, 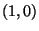 und
und 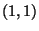 gebildet wird, und nennt
diesen Quotienten Gini-Koeffizient der (geordneten)
Stichprobe
gebildet wird, und nennt
diesen Quotienten Gini-Koeffizient der (geordneten)
Stichprobe
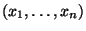 .
.
- Mit anderen Worten: Der Gini-Koeffizient
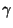 ist gegeben
durch
ist gegeben
durch
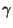 |
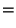 |
 |
|
| |
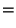 |
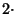 Flächeninhalt zwischen Diagonale und
Lorenzkurve Flächeninhalt zwischen Diagonale und
Lorenzkurve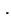 |
|
- Hieraus ergibt sich durch eine einfache Rechnung, dass
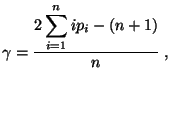 |
(11) |
wobei
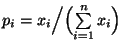 .
.
- Beachte
- Beispiel
- Für das obenbetrachtete Beispiel
der Marktanteile der 5 Unternehmen gilt
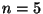 und
und
- Hieraus folgt, dass
bzw.
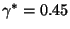 .
.




Next: Absolute und relative Häufigkeiten;
Up: Kenngrößen zur Beschreibung von
Previous: Maßzahlen für die Streuung
Contents
Hendrik Schmidt
2003-07-21
 nichtnegativ sind und
nichtnegativ sind und
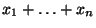 positiv
ist, d.h.
positiv
ist, d.h.
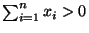 .
.
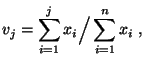
![\includegraphics[width=10cm]{wista_lorenz.eps}](img156.png)

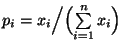 .
.