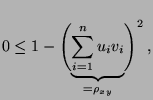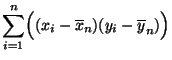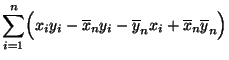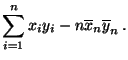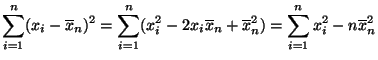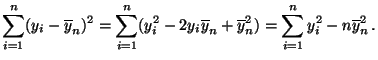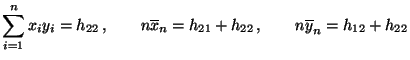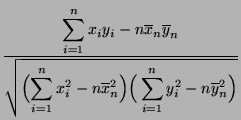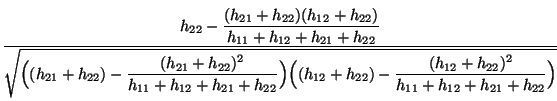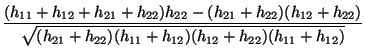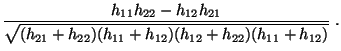Next: Ränge von Stichprobenwerten; Rang-Korrelationskoeffizient
Up: Beschreibung von metrischen bivariaten
Previous: Empirische Kovarianz; empirischer Korrelationskoeffizient
Contents
Herleitung der Formeln für 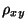
- Herleitung der Formel (24)
- Mit den abkürzenden Bezeichnungen
gilt offenbar
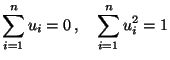
und
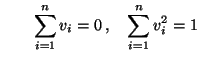
sowie
- Somit gilt für jedes
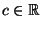
- Hieraus ergibt sich insbesondere für
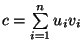 , dass
, dass
- Dies impliziert, dass
 bzw.
bzw.
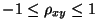 , womit die Gültigkeit von (24) bewiesen ist.
, womit die Gültigkeit von (24) bewiesen ist.
- Herleitung der Formel (25)
- Durch Ausmultiplizieren des Zählers in (23) ergibt
sich, dass
- Auf ähnliche Weise erhalten wir die Identitäten
und
- Wenn diese Ausdrücke in (23) eingesetzt werden,
ergibt sich nun mühelos die Formel (25).
- Herleitung der Formel (26)
- Für binäre Daten gilt offenbar
sowie
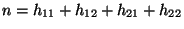 , wobei
, wobei 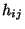 die in
Abschnitt 2.3.1 eingeführte absolute Häufigkeit ist.
die in
Abschnitt 2.3.1 eingeführte absolute Häufigkeit ist.
- Durch Einsetzen in (25) ergibt sich nun, dass
- Damit ist (26) bewiesen.
- Herleitung der Formel (28)




Next: Ränge von Stichprobenwerten; Rang-Korrelationskoeffizient
Up: Beschreibung von metrischen bivariaten
Previous: Empirische Kovarianz; empirischer Korrelationskoeffizient
Contents
Hendrik Schmidt
2003-07-21
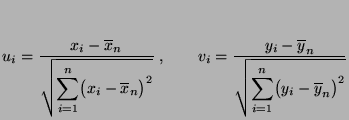
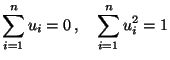 und
und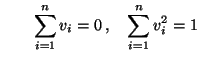
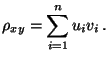
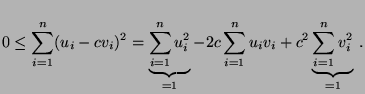
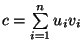 , dass
, dass