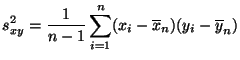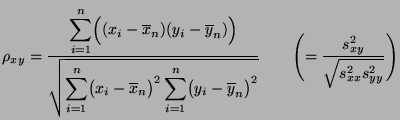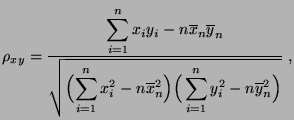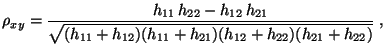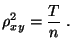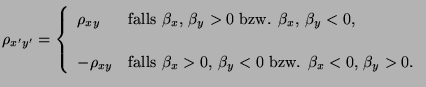- Aus dem Streudiagramm des Beispiels, das in
Abschnitt 2.4.1 betrachtet wurde, ergibt sich die
Vermutung, dass
- ein Zusammenhang zwischen den Merkmalen ,,Clusterzahl je Traube''
(
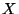 ) und ,,Jahresertrag''(
) und ,,Jahresertrag''(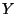 ) besteht, denn
) besteht, denn
- für wachsende Werte des Merkmals
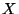 weist auch das Merkmal
weist auch das Merkmal 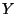 tendenzmäßig größere Werte auf.
tendenzmäßig größere Werte auf.
- ein Zusammenhang zwischen den Merkmalen ,,Clusterzahl je Traube''
(
- Eine Maßzahl zur Beschreibung eines solchen Zusammenhanges ist die
empirische Kovarianz
der Stichproben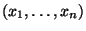 und
und
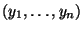 , wobei
die Stichprobenmittel von
, wobei
die Stichprobenmittel von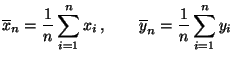
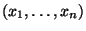 bzw.
bzw.
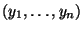 bezeichnen.
bezeichnen.
- Beachte
- Ein Nachteil des in (22) definierten
Zuhammenhangsmaßes besteht darin, dass
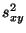 skalenabhängig
ist, d.h., von der Größe der Stichprobenwerte
skalenabhängig
ist, d.h., von der Größe der Stichprobenwerte
 bzw.
bzw.
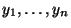 abhängt.
abhängt.
- Dieser Nachteil wird eliminiert, wenn anstelle der empirischen
Kovarianz
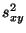 der empirische Korrelationskoeffizient
betrachtet wird.
der empirische Korrelationskoeffizient
betrachtet wird.
- Ein Nachteil des in (22) definierten
Zuhammenhangsmaßes besteht darin, dass
- Die Größe
heißt empirischer Korrelationskoeffizient der Stichproben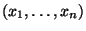 und
und
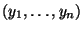 , wobei die
Stichprobenvarianzen
, wobei die
Stichprobenvarianzen 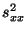 und
und 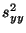 gegeben sind durch
gegeben sind durch
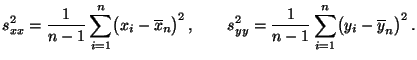
- Man kann zeigen, dass für den in (23) definierten
empirischen Korrelationskoeffizienten
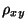 stets
stets
gilt, wobei-
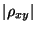 groß ist, wenn ein Zusammenhang zwischen
groß ist, wenn ein Zusammenhang zwischen 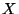 und
und 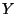 besteht, und
besteht, und
-
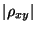 klein ist, wenn
klein ist, wenn 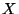 und
und 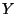 voneinander unabhängig
sind.
voneinander unabhängig
sind.
-
- Insbesondere kann man zeigen, dass
-
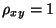 , falls sämtliche Punkte
, falls sämtliche Punkte
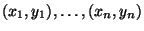 auf einer Geraden mit positivem Anstieg liegen,
auf einer Geraden mit positivem Anstieg liegen,
-
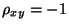 , falls sämtliche Punkte
, falls sämtliche Punkte
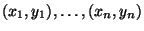 auf einer Geraden mit negativem
Anstieg liegen.
auf einer Geraden mit negativem
Anstieg liegen.
-
- Der empirische Korrelationskoeffizient
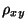 misst darüber
hinaus in dem folgenden Sinne die Stärke des linearen
Zusammenhanges zwischen den Ausprägungen/Werten der Merkmale
misst darüber
hinaus in dem folgenden Sinne die Stärke des linearen
Zusammenhanges zwischen den Ausprägungen/Werten der Merkmale 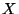 und
und 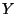 :
:
- Je näher die Punkte
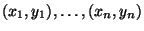 an einer Geraden
mit positivem Anstieg liegen, um so näher liegt der empirische
Korrelationskoeffizient
an einer Geraden
mit positivem Anstieg liegen, um so näher liegt der empirische
Korrelationskoeffizient 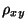 bei
bei 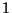 , und
, und
- je näher die Punkte
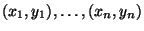 an einer Geraden
mit negativem Anstieg liegen, um so näher liegt der empirische
Korrelationskoeffizient
an einer Geraden
mit negativem Anstieg liegen, um so näher liegt der empirische
Korrelationskoeffizient 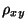 bei
bei 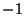 .
.
- Je näher die Punkte
- Eine (grobe) Klassifikation des Zusammenhanges der Merkmale
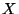 und
und 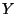 kann somit wie folgt beschrieben werden:
kann somit wie folgt beschrieben werden:
- ,,schwacher Zusammenhang'', falls
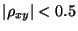 ,
,
- ,,mittlerer Zusammenhang'', falls
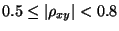 ,
,
- ,,starker Zusammenhang'', falls
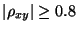 .
.
- ,,schwacher Zusammenhang'', falls
- Man kann zeigen, dass sich der in (23) definierte
empirische Korrelationskoeffizient
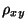 darstellen lässt in
der Form
darstellen lässt in
der Form
wobei diese alternative Darstellung des empirischen Korrelationskoeffizienten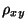 günstiger für das praktische
Rechnen ist.
günstiger für das praktische
Rechnen ist.
- Übungsaufgabe. Bestimmen Sie für die in
Abschnitt 2.4.1 betrachteten Daten über den
Jahresertrag bzw. die mittlere Clusterzahl je Traube
- die Stichprobenmittel
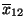 und
und
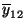 sowie
sowie
- den empirischen Korrelationskoeffizienten
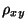 .
.
- die Stichprobenmittel
- Außerdem lässt sich für binäre Daten, d.h., falls die
Stichprobenwerte
 und
und
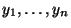 nur 0
oder
nur 0
oder 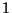 sein können, noch eine weitere nützliche
Darstellungsformel für den empirischen Korrelationskoeffizienten
sein können, noch eine weitere nützliche
Darstellungsformel für den empirischen Korrelationskoeffizienten
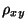 angeben.
angeben.
- Mit der in Abschnitt 2.3.1 eingeführten Notation gilt
dann
wobei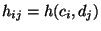 für jedes
für jedes
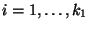 unf für jedes
unf für jedes
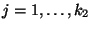 die absolute Häufigkeit bezeichnet, mit der die
Kombination
die absolute Häufigkeit bezeichnet, mit der die
Kombination 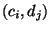 der Ausprägungen
der Ausprägungen
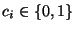 und
und
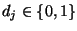 in den Stichproben
in den Stichproben
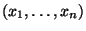 bzw.
bzw.
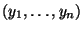 auftritt.
auftritt.
- Beachte
- Wenn man die Formeln (18) und
(26) miteinander vergleicht, dann erkennt man, dass
der
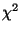 -Koeffizient
-Koeffizient 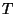 und der empirische
Korrelationskoeffizient
und der empirische
Korrelationskoeffizient 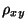 bei binären Daten wie folgt
zusammenhängen: Es gilt
bei binären Daten wie folgt
zusammenhängen: Es gilt
- Wir betrachten nun erneut das in Abschnitt 2.3.1
eingeführte Beispiel mit den Ausprägungen ,,keine Ausbildung''
bzw. ,,Lehre'' für das Merkmal ,,Ausbildungsniveau'' sowie den
Ausprägungen ,,mittelfristige Arbeitslosigkeit'' (7-12 Monate)
bzw. ,,langfristige Arbeitslosigkeit (
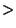 12 Monate) für das
Merkmal ,,Dauer der Arbeitslosigkeit''.
12 Monate) für das
Merkmal ,,Dauer der Arbeitslosigkeit''.
- Wenn wir dabei die Eintragungen der
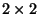 -Kontingenztafel (20) in die Darstellungsformel
(26) einsetzen, dann ergibt sich, dass
-Kontingenztafel (20) in die Darstellungsformel
(26) einsetzen, dann ergibt sich, dass
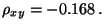
- Hieraus und aus (27) ergibt sich darüber hinaus,
dass
was mit dem Ergebnis (21) übereinstimmt, das bereits am Ende von Abschnitt 2.3.3 ermittelt wurde.
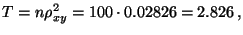
- Wenn man die Formeln (18) und
(26) miteinander vergleicht, dann erkennt man, dass
der
- Die Deutung des empirischen Korrelationskoeffizienten
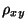 als Maßzahl zur Quantifizierung des (linearen) Zusammenhanges
zwischen den Ausprägungen zweier Merkmale
als Maßzahl zur Quantifizierung des (linearen) Zusammenhanges
zwischen den Ausprägungen zweier Merkmale 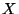 und
und 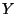 wird auch
durch die folgende Invarianzeigenschaft von
wird auch
durch die folgende Invarianzeigenschaft von
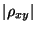 bei linearer Daten-Transformation gestützt.
bei linearer Daten-Transformation gestützt.
- Außer den ursprünglichen Stichprobenwerten
 bzw.
bzw.
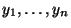 betrachten wir noch die linear
transformierten Stichprobenwerte
betrachten wir noch die linear
transformierten Stichprobenwerte
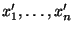 bzw.
bzw.
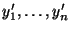 , wobei
, wobei
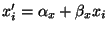 bzw.
bzw.
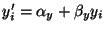 für jedes
für jedes
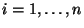 und für
gewisse Konstanten
und für
gewisse Konstanten
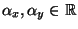 und
und
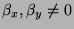 .
.
- Es gilt dann