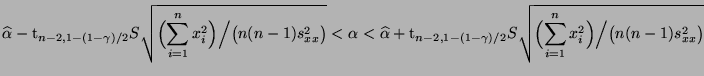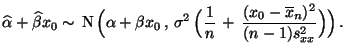- Zur Erinnerung: Bei der Konstruktion von Konfidenzintervallen für (reellwertige) Modellparameter, die auch
Vertrauensintervalle genannt werden, geht man wie folgt vor.
- Man betrachtet zwei Abbildungen
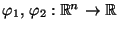 , die den beobachteten Daten
, die den beobachteten Daten
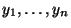 , d.h. jeder Realisierung
, d.h. jeder Realisierung
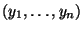 der
Zufallsstichprobe
der
Zufallsstichprobe
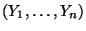 , die Schätzwerte
, die Schätzwerte
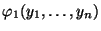 bzw.
bzw.
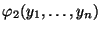 zuordnen, und zwar so, dass
zuordnen, und zwar so, dass
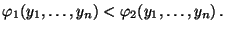
- Die zugehörigen Schätzer
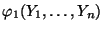 und
und
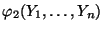 ergeben dann ein zufälliges
Intervall
ergeben dann ein zufälliges
Intervall
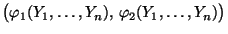 ,
das den unbekannten Modellparameter
,
das den unbekannten Modellparameter
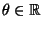 (zumindest) mit
einer vorgegebenen Überdeckungswahrscheinlichkeit
(zumindest) mit
einer vorgegebenen Überdeckungswahrscheinlichkeit
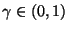 enthalten soll.
enthalten soll.
- Mit anderen Worten: Die Schätzer
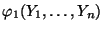 und
und
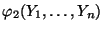 liefern ein Konfidenzintervall
für
liefern ein Konfidenzintervall
für 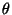 zum Niveau
zum Niveau 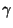 , falls
, falls
- Die ,,Nichtüberdeckungswahrscheinlichkeit''
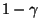 wird Irrtumswahrscheinlichkeit genannt. Sie entspricht der in
Abschnitt 3.1.3 betrachteten Fehlerwahrscheinlichkeit
erster Art.
wird Irrtumswahrscheinlichkeit genannt. Sie entspricht der in
Abschnitt 3.1.3 betrachteten Fehlerwahrscheinlichkeit
erster Art.
- Man betrachtet zwei Abbildungen
- Aus (16) und (17) ergeben sich ohne
weiteres die folgenden Konfindenzintervalle zum Niveau
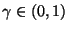 für die Modellparameter
für die Modellparameter 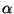 und
und 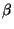 . Und
zwar gilt jeweils mit Wahrscheinlichkeit
. Und
zwar gilt jeweils mit Wahrscheinlichkeit 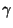
und
- Beispiele
- i)
- Zusammenhang von Weglänge und Lieferzeit
- Für die in Abschnitt 3.1.3 betrachteten Daten über Weglängen und Lieferzeiten von 10 zufällig ausgewählten Lkw-Lieferungen hatten wir gezeigt, dass der Zusammenhang von Weglänge und Lieferzeit statistisch signifikant ist.
- Außerdem hatten wir gezeigt, dass
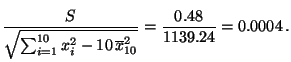
- Aus (25) ergibt sich somit das folgende
Konfidenzintervall für
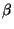 zum Niveau
zum Niveau
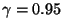 :
:
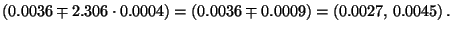
- ii)
- Zusammenhang von Geburtsgewicht und
Gewichtszunahme
- Wir betrachten erneut die Daten über die Merkmale ,,Geburtsgewicht'' von Säuglingen sowie deren ,,Gewichtszunahme'' zwischen dem 70. und 100. Tag, für die in Abschnitt 3.1.3 ein statistisch signifikanter Zusammenhang zwischen diesen beiden Merkmalen ermittelt wurde.
- Aus (25) ergibt sich das folgende
Konfidenzintervall für
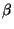 zum Niveau
zum Niveau
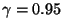 :
:
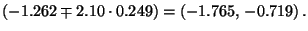
- Auf ähnliche Weise kann man auch ein Konfidenzintervall zum Niveau
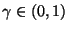 für den erwarteten Zielwert
für den erwarteten Zielwert
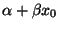 herleiten, der einem vorgegebenen Ausgangswert
herleiten, der einem vorgegebenen Ausgangswert
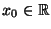 entspricht.
entspricht.
- Von besonderem Interesse ist dabei natürlich der Fall, dass
 , d.h., wenn an der Stelle
, d.h., wenn an der Stelle 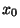 keine Daten erhoben werden.
keine Daten erhoben werden.
- Sei also
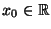 eine (geeignet gewählte) reelle Zahl mit
eine (geeignet gewählte) reelle Zahl mit
- Dann ist durch den Ansatz
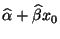 ein
erwartungstreuer Schätzer für
ein
erwartungstreuer Schätzer für
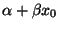 gegeben mit
gegeben mit
- Mit Wahrscheinlichkeit
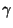 gilt somit, dass
gilt somit, dass
wobei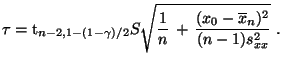
- Von besonderem Interesse ist dabei natürlich der Fall, dass
- Beachte
- Bei gegebenen Daten
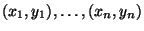 ist die Länge des
in (28) hergeleiteten Konfidenzintervalls für
ist die Länge des
in (28) hergeleiteten Konfidenzintervalls für
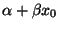 eine monoton nichtfallende Funktion des
Abstandes
eine monoton nichtfallende Funktion des
Abstandes
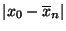 , die ihr Minimum im Punkt
, die ihr Minimum im Punkt
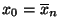 annimmt.
annimmt.
- Die in (28) hergeleitete Intervallschätzung für
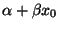 ist also dann am genauesten, wenn der Wert
ist also dann am genauesten, wenn der Wert
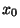 im ,,Zentrum'' der (Ausgangs-) Werte
im ,,Zentrum'' der (Ausgangs-) Werte
 liegt.
liegt.
- Andererseits können Ergebnisse entstehen, die offenkundig falsch
sind, falls
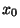 eine der beiden Ungleichungen in
(26) nicht erfüllt.
eine der beiden Ungleichungen in
(26) nicht erfüllt.
- So würde sich aus den Daten über die Merkmale Geburtsgewicht von
Säuglingen und deren Gewichtszunahme beispielsweise für das
,,Geburtsgewicht''
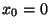 eine geschätzte Gewichtszunahme von
eine geschätzte Gewichtszunahme von
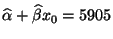 ergeben.
ergeben.
- Bei gegebenen Daten
- Beispiel
- Aus den in Abschnitt 3.1.3 betrachteten Daten über
Weglängen und Lieferzeiten von 10 zufällig ausgewählten
Lkw-Lieferungen ergibt sich für die Weglänge
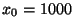 , dass
, dass

- Außerdem gilt
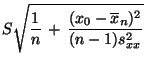
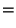
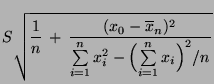
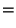
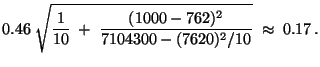
- Aus (28) ergibt sich somit das folgende
Konfidenzintervall zum Niveau
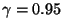 für die erwartete
Lieferzeit
für die erwartete
Lieferzeit
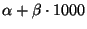 bei der (angenommenen)
Weglänge von
bei der (angenommenen)
Weglänge von 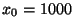 :
:
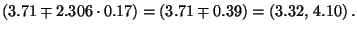
- Aus den in Abschnitt 3.1.3 betrachteten Daten über
Weglängen und Lieferzeiten von 10 zufällig ausgewählten
Lkw-Lieferungen ergibt sich für die Weglänge