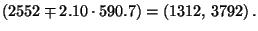- der (unbekannte) Erwartungswert
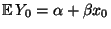 der
Zufallsvariable
der
Zufallsvariable
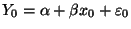 mit der
(vorgegebenen) Wahrscheinlichkeit
mit der
(vorgegebenen) Wahrscheinlichkeit 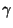 liegt, wobei
liegt, wobei
- die Störgröße
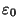 normalverteilt und unabhängig von den
Störgrößen
normalverteilt und unabhängig von den
Störgrößen
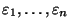 ist;
ist;
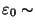 N
N
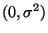 .
.
- Dabei seien
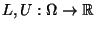 zwei Zufallsvariablen, so dass
zwei Zufallsvariablen, so dass
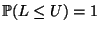 und
und
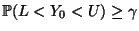 gilt.
gilt.
- Das zufällige Intervall
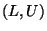 wird dann Prognoseintervall
für die Zielvariable
wird dann Prognoseintervall
für die Zielvariable 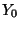 zum Niveau
zum Niveau 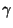 genannt.
genannt.
gilt, wobei
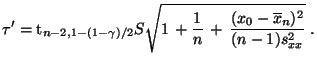
- Aus den in Abschnitt 2.4.4 betrachteten Daten über die
Merkmale ,,Geburtsgewicht'' von Säuglingen sowie deren
,,Gewichtszunahme'' zwischen dem 70. und 100. Tag ergibt sich,
dass
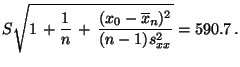
- Aus (29) ergibt sich somit das folgende
Prognoseintervall zum Niveau
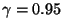 für die
Gewichtszunahme
für die
Gewichtszunahme
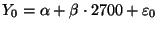 bei dem
(angenommenen) Geburtsgewicht von
bei dem
(angenommenen) Geburtsgewicht von 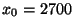 :
: