



Next: Kleinste-Quadrate-Schätzer bei zwei Einflussfaktoren
Up: Multiple lineare Regression
Previous: Multiple lineare Regression
Contents
Modellbeschreibung
- Wir betrachten die folgende Verallgemeinerung des in
Abschnitt 3.1 diskutierten (einfachen) linearen
Regressionsmodells mit deterministischen Ausgangswerten
 eines einzelnen Einflussfaktors.
eines einzelnen Einflussfaktors.
- Dabei lassen wir nun zu, dass die Zielvariablen
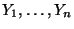 nicht nur von den Werten
nicht nur von den Werten
 eines einzelnen
Einflussfaktors abhängen, d.h., wir betrachten
eines einzelnen
Einflussfaktors abhängen, d.h., wir betrachten 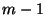 Einflussfaktoren, wobei
Einflussfaktoren, wobei 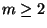 eine beliebige, jedoch fest
vorgegebene natürliche Zahl ist;
eine beliebige, jedoch fest
vorgegebene natürliche Zahl ist;  .
.
- Mit anderen Worten: Wir nehmen an, dass die Zielvariablen
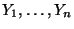 von
von 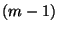 -dimensionalen vektoriellen
Ausgangswerten
-dimensionalen vektoriellen
Ausgangswerten
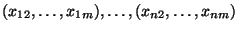 abhängen,
d.h., es gelte
abhängen,
d.h., es gelte
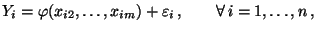 |
(51) |
wobei
- Die unbekannten Modellparameter
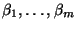 und
und
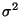 sind aus den vorliegenden Daten
sind aus den vorliegenden Daten
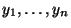 bzw.
bzw.
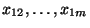 ,
, 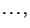
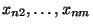 zu
schätzen.
zu
schätzen.
- Beachte
- In Matrixschreibweise lässt sich das in
(51) und (52) gegebene multiple
lineare Regressionsmodell wie folgt formulieren:
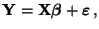 |
(54) |
wobei
 |
(55) |
- Dabei wird
 die Designmatrix des Regressionsmodells
genannt.
die Designmatrix des Regressionsmodells
genannt.




Next: Kleinste-Quadrate-Schätzer bei zwei Einflussfaktoren
Up: Multiple lineare Regression
Previous: Multiple lineare Regression
Contents
Hendrik Schmidt
2003-07-21
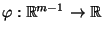 gegeben ist
durch
gegeben ist
durch
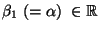 und den
Regressionskoeffizienten
und den
Regressionskoeffizienten
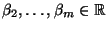 ,
,
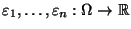 unabhängig sind mit
unabhängig sind mit
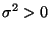 .
.