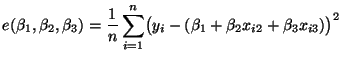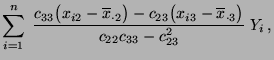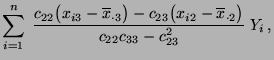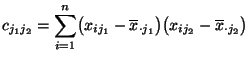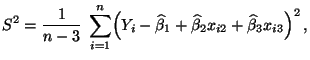bzw. durch partielle Differentiation der Funktion
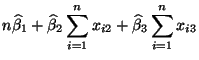 |
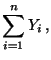 |
||
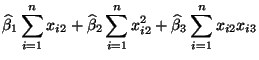 |
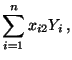 |
||
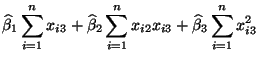 |
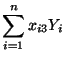 |
genügen müssen, deren Lösung gegeben ist durch
- wobei
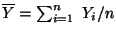 bzw.
bzw.
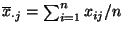 für
für 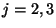 und
und
- und wobei vorausgesetzt wird, dass
- Die Bedingung (59) ist gleichbedeutend damit, dass
die Designmatrix
vollen Spaltenrang
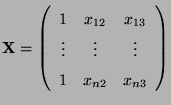
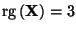 hat, d.h., dass
hat, d.h., dass
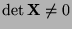 bzw. dass
bzw. dass
 aus drei linear unabhängigen
Spaltenvektoren besteht.
aus drei linear unabhängigen
Spaltenvektoren besteht.
- Man kann zeigen, dass die Kleinste-Quadrate-Schätzer
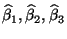 für
für
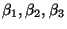 erwartungstreu sind, d.h., es gilt
erwartungstreu sind, d.h., es gilt
- Die (zufällige) Abbildung
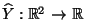 mit
mit
die jedem Wertepaar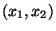 der beiden Einflussfaktoren die
Zufallsvariable
der beiden Einflussfaktoren die
Zufallsvariable
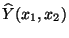 zuordnet, heißt empirische Regressionsebene.
zuordnet, heißt empirische Regressionsebene.
- Außerdem kann man zeigen, dass die ,,Reststreueung''
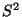 um die
empirische Regressionsebene, die gegeben ist durch
um die
empirische Regressionsebene, die gegeben ist durch
ein erwartungstreuer Schätzer für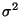 ist, d.h., es gilt
ist, d.h., es gilt
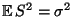 .
.
- In einem Unternehmen der Metallindustrie soll untersucht werden, inwiefern die Güte eines Erzeugnisses von zwei technologischen (Einfluss-) Faktoren des Produktionsprozesses abhängt.
- Dabei wird die Stahlproduktion eines Stahlwerkes betrachtet, wobei die Stahlausbeute (Zielvariable, gemessen in Prozent) in Abhängigkeit von der Anzahl der bisher erfolgten Abstiche (1.Einflussfaktor) und dem Schwefelgehalt (2. Einflussfaktor, gemessen in Prozent) untersucht wird.
- Die Qualitätskennzahl ,,Stahlausbeute'' wurde für 26 Proben des
Erzeugnisses bestimmt, wobei für die technologischen
Einflussfaktoren ,,Anzahl der Abstiche'' bzw. ,,Schwefelgehalt''
jeweils unterschiedliche (Ausgangs-) Werte beobachtet wurden:
Nummer der Probe 1 2 3 4 5 6 7 8 9 10 11 12 13 Wert des 1. Faktors 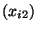
53 34 39 39 28 39 39 15 19 27 23 24 25 Wert des 2. Faktors 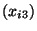
8 8 7 9 9 8 9 12 12 8 8 8 8 Qualitätskennzahl 
19 70 0 77 85 70 0 100 78 78 98 59 87 Nummer der Probe 14 15 16 17 18 19 20 21 22 23 24 25 26 Wert des 1. Faktors 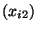
27 9 37 20 23 11 10 13 45 6 7 15 22 Wert des 2. Faktors 
8 7 25 10 9 7 9 8 13 12 7 12 11 Qualitätskennzahl 
70 100 42 96 76 82 100 97 68 92 95 96 91 - Aus diesen Daten ergeben sich die folgenden Werte für die Größen,
die in den Definitionsgleichungen (57) der Schätzer
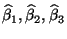 vorkommen:
vorkommen:
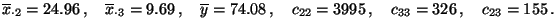
- Durch Einsetzen der ermittelten Werte in (57)
ergibt sich nun, dass
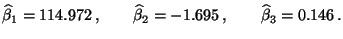
- Somit erhalten wir die geschätzte Regressionsebene
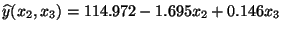 :
:
![\includegraphics[width=7cm]{wista_regplane.eps}](img904.png)
- Für die in (62) betrachtete Restreueung
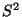 ergibt sich schließlich der Schätzwert
ergibt sich schließlich der Schätzwert
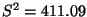 bzw.
bzw.
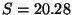 .
.