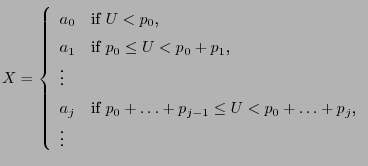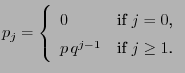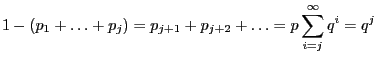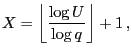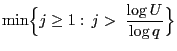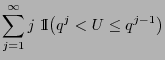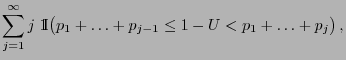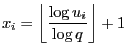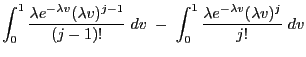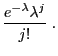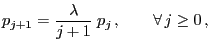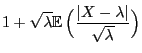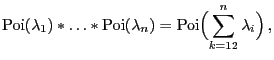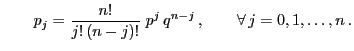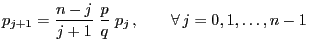Next: Acceptance-Rejection Method
Up: Transformation of Uniformly Distributed
Previous: Inversion Method
Contents
Transformation Algorithms for Discrete Distributions
- Example
 (geometric distribution)
(geometric distribution)
For some discrete distributions there are specific
transformation algorithms allowing the generation of
pseudo-random numbers having this distribution.
- Examples
-
- Poisson distribution
 (with small expectation
(with small expectation 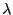 )
)
- Poisson distribution
 (with large expectation
(with large expectation 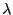 )
)
- Binomial distribution




Next: Acceptance-Rejection Method
Up: Transformation of Uniformly Distributed
Previous: Inversion Method
Contents
Ursa Pantle
2006-07-20
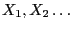
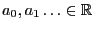 with probabilities
with probabilities
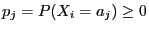 for
for
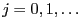 ,
,
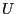 be a
be a ![$ (0,1]$](img165.png) -uniformly distributed random variable and
let the random variable
-uniformly distributed random variable and
let the random variable 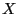 be given by
be given by
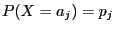 for all
for all
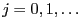 .
.
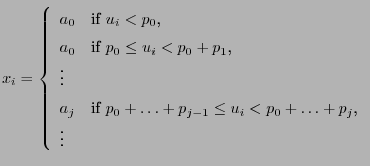
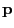 -distributed random variables where
-distributed random variables where 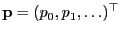 ,
,
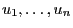 are realizations of independent and uniformly
distributed random variables on
are realizations of independent and uniformly
distributed random variables on ![$ (0,1]$](img165.png) .
.