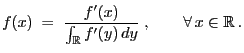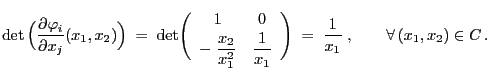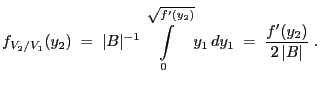Next: Simulation Methods Based on
Up: Transformation of Uniformly Distributed
Previous: Acceptance-Rejection Method
Contents
Quotients of Uniformly Distributed Random Variables
In many cases random variables having absolutely continuous
distributions can be represented as quotients of uniformly
distributed random variables.
- Combined with acceptance-rejection sampling (see
Section 3.2.3) this yields another type of simulation
algorithm.
- The mathematical foundation for this type of algorithm is the
following transformation theorem for the density of absolutely
continuous random vectors (that has already been mentioned e.g. in
Section 1.2.3 of the course ,,Statistik I'').
From Theorem 3.8 we obtain the following result
concerning the representation of absolutely continuous random
variables as quotients of uniformly distributed random variables.
Theorem 3.9
- Let
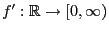 be Borel measurable and bounded such
that
be Borel measurable and bounded such
that
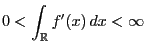 and and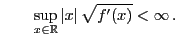 |
(27) |
- Let the random vector
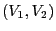 be uniformly distributed on the
(bounded) Borel set
be uniformly distributed on the
(bounded) Borel set
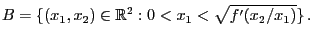 |
(28) |
- Then the quotient
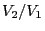 is an absolutely continuous random
variable with density
is an absolutely continuous random
variable with density
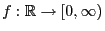 where
where
- Proof
-
- Example
 (normal distribution)
(normal distribution)




Next: Simulation Methods Based on
Up: Transformation of Uniformly Distributed
Previous: Acceptance-Rejection Method
Contents
Ursa Pantle
2006-07-20
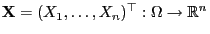 be an absolutely
continuous random vector with joint density
be an absolutely
continuous random vector with joint density
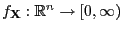 and let
and let
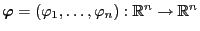 be a
Borel-measurable function with continuous partial derivatives
be a
Borel-measurable function with continuous partial derivatives
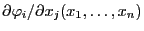 .
.
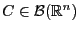 be picked in a way such
that
and
be picked in a way such
that
and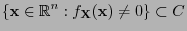 which ensures that the restriction
which ensures that the restriction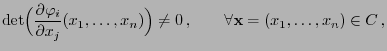
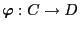 of
of
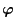 to the set
to the set 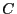 is a bijection where
is a bijection where
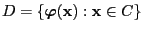 denotes the image of
denotes the image of
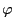 .
.
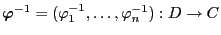 be the inverse of
be the inverse of
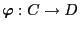 .
.
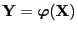 is also absolutely
continuous and the density
is also absolutely
continuous and the density
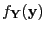 of
of
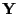 is given by
is given by
![$\displaystyle f_{\mathbf{Y}}({\mathbf{y}})=\left\{\begin{array}{ll} f_{\mathbf{...
...D$,}\\ [3\jot] 0\,, & \mbox{falls ${\mathbf{y}}\not\in D$.} \end{array}\right.$](img1467.png)
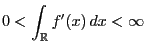 and
and