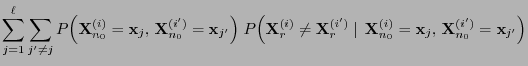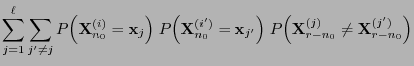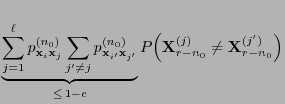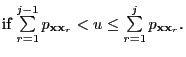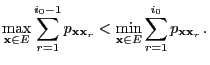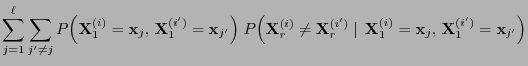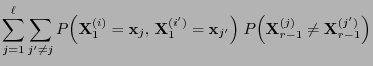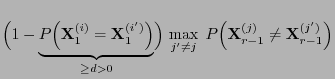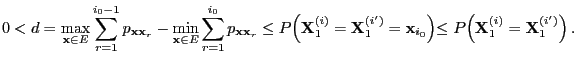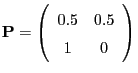- is running forward, i.e. in a way that is perceived as natural.
- Therefore, one also refers to this method as coupling to the future.
- with deterministic initial state
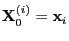 and with an
irreducible and aperiodic transition matrix
and with an
irreducible and aperiodic transition matrix
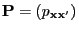 ,
,
- such that
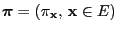 is the ergodic limit
distribution of the Markov chain
is the ergodic limit
distribution of the Markov chain
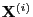 .
.