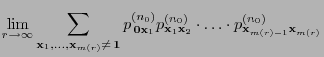- (a)
-
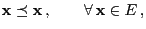
- (b)
-
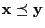 and
and
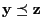
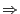
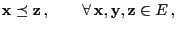
- (c)
-
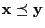 and
and
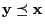
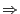
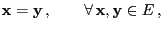
- (d)
-
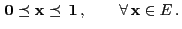
- that the update function
![$ \varphi:E\times(0,1]\to E$](img173.png) is monotonously nondecreasing with respect to the partial order
is monotonously nondecreasing with respect to the partial order
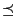 , i.e., for arbitrary
, i.e., for arbitrary
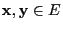 such that
such that
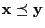 we have
we have
- i.e., we merely consider a single sequence
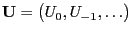 of independent and
of independent and
![$ (0,1]$](img165.png) -uniformly distributed random variables and define
-uniformly distributed random variables and define
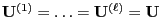 .
.
- For arbitrary
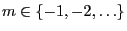 and
and
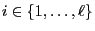 the
Markov chain
the
Markov chain
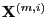 is recursively defined by
is recursively defined by